
Archives
Cercle de lecture des Coniques d'Apollonios
Les différents articles qui suivent, sont issus des travaux du Cercle qui s’était lancé dans une lecture hebdomadaire du texte des Coniques d’Apollonios au début des années 1990. Après la lecture des livres I à VII, cette lecture s’est poursuivie jusqu’en 2023 avec comme objectif la traduction et la lecture du livre VIII restitué par Edmund Halley.
Vous y trouverez les articles suivants :
Résumé du Livre I des Coniques d'Apollonios
Le premier livre des Coniques est introduit par une lettre à un certain Eudème, personnage inconnu par ailleurs. Il faut en fait la comprendre comme une préface, car après quelques propos amicaux, Apollonios y présente surtout les huit livres de son œuvre.
Les résultats nouveaux ne sont pas dans les deux premiers livres mais ils composent la plupart des théorèmes du troisième. C’est là l’opinion d’Apollonios mais elle demande à être nuancée. Au commencement du premier livre, nous lisons que le cône se fonde sur une nouvelle définition. Il s’ensuit donc une exposition qui, eu égard à cette définition, est nouvelle. C’est pour nous comme pour les premiers lecteurs d’Apollonios la valeur principale des premiers livres. À nos yeux, il en est d’autres. La définition du cône, selon Apollonios, fait naître une seconde nappe à ce solide, impliquant, par là même, toute une série de résultats en relation avec la toute nouvelle seconde branche des hyperboles. De notre point de vue, il y a donc des résultats nouveaux. Apollonios les voyait peut être comme une généralisation à la seconde branche de résultats qui pouvaient être plus anciens. Il nous écrit, sans les préciser, que des propriétés seront exposées d’une manière plus développée et plus générale que chez d’autres qui ont écrit sur la [même] matière. Son choix de ne pas les reconnaître comme nouveaux est alors compréhensible. Mais cet argument vaut-il aussi pour les hyperboles conjuguées ? Elles induisent des résultats que, sans aucun doute possible, nous devons à Apollonios et à lui seul et qui ne sont le développement d’aucun autre. Pourtant, à y regarder de près, il s’agit encore de généraliser à de nouvelles hyperboles des résultats connus sur une seule branche. Notre jugement serait plus assuré si nous pouvions comparer l’œuvre d’Apollonios à celles de ses prédécesseurs. Nous verrions plus clairement qu’elle est la manière plus développée et plus générale de certaines propriétés. Hélas, bien peu de résultats relatifs à la science pré-apollonienne des coniques ont subsisté jusqu’à nous. Tout au plus quelques traces, tant l’œuvre d’Apollonios a rapidement et presque totalement éclipsé les acquis de ses prédécesseurs.
Les huit livres d’Apollonios font apparaître la première étude des coniques s’appuyant sur les cônes les plus généraux. Ils rassemblent aussi une somme de résultats qui ne seront pas égalés avant le XVIIème siècle, c’est-à-dire, pendant deux mille ans. Dès le premier livre, nous rencontrons des résultats profonds sur l’hyperbole complète, avec ses deux branches, sur les diamètres et les hyperboles conjugués, nous découvrons tous les axes possibles de chaque conique et même le moyen permettant le passage de relations métriques d’un axe à l’autre. Nous voyons donc naître une idée qui, bien plus tard, trouvera sa place dans les changements de repère.
Ce commentaire ne reprendra pas toutes les parties qui composent le premier livre mais se limitera à rappeler quelques différences essentielles entre le style d’Apollonios et le nôtre, à expliquer la formation de certaines des relations métriques tout en soulignant l’importance du cercle en arrière plan de cette étude, et enfin à traiter du cas des tangentes dans une géométrie qui ignorait tout des dérivées.
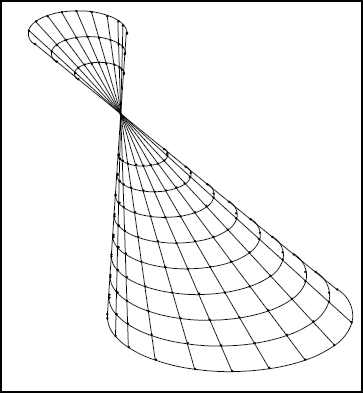
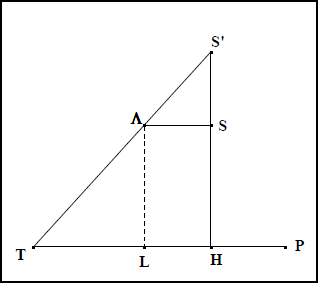
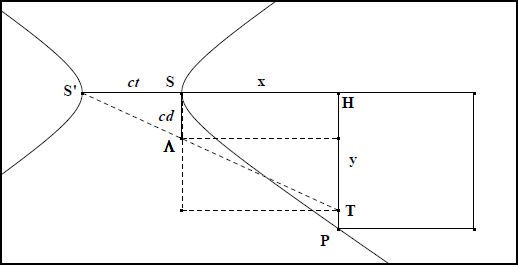
Sans entrer dans le détail des connaissances que le temps avait permis d’accumuler, la lettre-préface nous apprend que le contenu des quatre premiers livres, bien que considérable, n’était pas nouveau, et que leur originalité tiendrait surtout à une disposition différente des propositions et à une définition du cône, plus générale que la définition antérieure. Apollonios, en effet, propose de définir la surface conique par la mouvement d’une droite s’appuyant sur la circonférence d’un cercle, qui en sera la base, et passant par un point fixe, qui sera le sommet du cône (fig. IIa 1). Nous reconnaissons là une définition toujours actuelle et nous la lui devons. Qu’en était-il alors de la définition antérieure ? Nous la connaissons grâce aux Éléments d’Euclide qui furent rédigés un siècle, environ, avant l’ouvrage d’Apollonios.
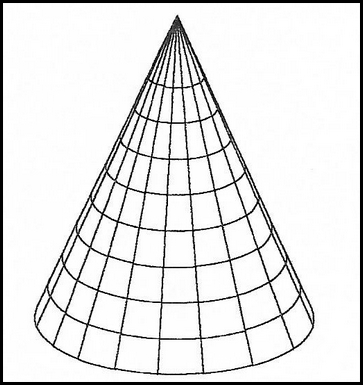
Le cône, lisons-nous, est engendré par la rotation d’un triangle rectangle autour de l’un de ses côtés perpendiculaires, la surface conique étant décrite par l’hypoténuse et le cercle de base par le troisième côté (fig. IIa 2). Ajoutons que cette définition ne prenait pas en compte la possibilité d’une seconde nappe, que, dans les Éléments, son objectif était de permettre l’évaluation du volume conique, et que, dans nos collèges, c’est elle que l’on enseigne et dans le même but.
L’étude des courbes engendrées par des sections planes du cône, s’appuyait, avant Apollonios, sur la définition d’un cône de révolution à une seule nappe. On sait aussi que les plans de coupe étaient particuliers, car toujours perpendiculaires à une génératrice et que les dénominations des différentes intersections, connues aujourd’hui sous les noms apolloniens de parabole, d’ellipse et d’hyperbole, provenaient d’une répartition des cônes de révolution en trois ensembles distincts. En vue de l’étude des coniques, seule la coupe d’un cône dont l’angle au sommet était droit, c’est-à-dire, dont l’angle compris entre deux génératrices diamétralement opposées sur le cercle de base était droit, proposait une parabole (fig. IIa 3). C’est bien pourquoi, avant Apollonios, elle portait le nom de section de cône rectangle. Quant à l’ellipse et à l’hyperbole, la première provenait seulement des cônes dont l’angle au sommet était aigu et portait de ce fait le nom de section de cône acutangle (fig. IIa 4) et la seconde, seulement des cônes dont l’angle au sommet était obtus et portait donc le nom de section de cône obtusangle (fig. IIa 5).
Toutes ces distinctions prendront fin avec Apollonios : tout plan de l’espace pourra donner une section conique, quel que soit le cône. Désormais, le genre de la conique ne dépend plus du cône mais de la position du plan qui coupe le cône. Précisément, suivant que ce plan est parallèle à la génératrice diamétralement opposée à celle passant par le sommet de la section, ou la rencontre en deçà du sommet ou au delà, on obtient dans le même ordre, une parabole, une ellipse ou une hyperbole, cette dernière devenant une section à deux branches. Le procédé est toujours d’actualité et figure même dans des dictionnaires comme le Petit Larousse.
Dans la période qui précède immédiatement la rédaction des Coniques par Apollonios, les sections sont toutes nommées « paraboles », et sont distinguées entre elles par les mentions « par excès », « par égalité » ou « par défaut » ; selon certains commentateurs, le mot parabole dériverait d’un verbe signifiant « appliquer exactement », le mot ellipse dériverait du verbe « souspasser », « être en manque » ou « faire défaut » et le mot hyperbole du verbe « surpasser ». Ces expressions font référence à certaines propriétés des trois courbes, obtenues par le procédé dit « d’application des aires ».
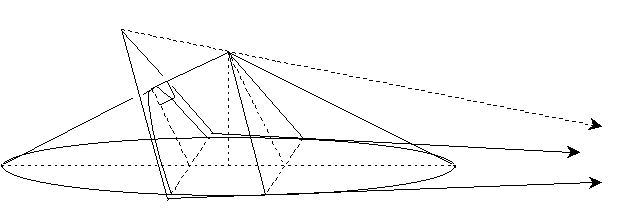
Le premier livre des Coniques commence comme un chapitre de géométrie dans l’espace. Les premières propositions nous présentent les sections coniques à partir de l’intersection du cône avec des plans. La troisième proposition montre que la section peut être un triangle, les deux propositions suivantes qu’elle peut être un cercle, à savoir la quatrième en considérant une section parallèle à la base du cône et la cinquième par une section dite antiparallèle qui ne se distingue de la précédente que dans les cônes obliques et que nous devons donc à Apollonios. La neuvième proposition établit que toutes les autres sections ne seront jamais des cercles et enfin les onzième, douzième et treizième montrent que ces sections non circulaires, sont respectivement des paraboles, des ellipses ou des hyperboles. A partir de la quinzième proposition, la présence du cône n’étant plus nécessaire à la disposition des éléments du discours, il disparaît et l’étude des coniques se poursuit désormais dans le cadre mieux adapté de la géométrie plane.
La rédaction d’Apollonios respecte la structure et le style euclidien : énoncé de la propriété en termes généraux ; introduction à la démonstration au moyen d’une figure qui précise et nomme les éléments utiles au discours ; énonciation claire, dans le cadre défini par la figure, de la propriété à démontrer ; démonstration proprement dite et conclusion qui, comme chez Euclide, est souvent sous-entendue. Sa mathématique sous-entend souvent que le lecteur connaît les Éléments d’Euclide, en particulier le deuxième livre sur l’ « algèbre » des grandeurs, le cinquième sur les rapports de grandeurs et le sixième sur les rapports de longueurs. Le lecteur, peu habitué aux mathématiques euclidiennes doit conserver à l’esprit que les grandeurs que nous comprenons comme des nombres, tant la notion de mesure nous est familière, n’en sont pas pour nos ancêtres. La substitution d’une mesure aux grandeurs suppose l’existence d’une mesure unité, commune à toutes les grandeurs de même nature. Or, on le savait bien, la diagonale d’un carré ne se compare pas en mesure avec son côté ; leur rapport n’est pas un nombre rationnel et donc il n’est pas un nombre pour nos ancêtres. Soyons humbles ! Ils ne deviendront rigoureusement des nombres que lors du XIXe siècle. C’est donc par un souci de rigueur que l’« algèbre » employée par Apollonios dans la conduite des calculs ajoute une démarche lente et complexe à l’usage peu commode d’une écriture ignorante des notations modernes. A nos yeux, des expressions tels « le rectangle de deux longueurs » est immédiatement traduite en produit de deux nombres et d’autres, tels les compositions de rapports en produits de fractions. Si donc, nous appliquons spontanément et avec raison des règles algébriques qui nous simplifient considérablement les calculs apolloniens, n’oublions pas cependant qu’elles sont anachroniques.
Apollonios utilise de manière récurrente quelques résultats du corpus euclidien, parmi lesquels, les cinquième et sixième propositions du livre II des Éléments et la vingt-troisième du livre VI. Ces trois propositions interviennent lors des manipulations algébriques sur les grandeurs, celle du livre VI lui procurant des règles algébriques pour simplifier des produits de rapports ou pour trouver des rapports équivalents. Dans notre algèbre, il s’agit de l’égalité : ![]() .
.
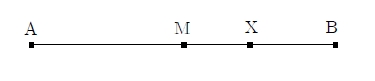
En commençant par la cinquième, celles du livre II s’énoncent de manière moderne dans les termes suivants :
Tout point ![]() d’un segment
d’un segment ![]() forme avec les extrémités et le milieu
forme avec les extrémités et le milieu ![]() l’identité suivante :
l’identité suivante :
![]()
 En notant la mesure du demi-segment par
En notant la mesure du demi-segment par Si le point ![]() est à l’extérieur, la sixième proposition énonce que :
est à l’extérieur, la sixième proposition énonce que :
![]()
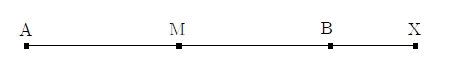 Avec les mêmes notations :
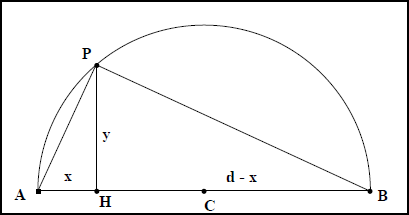
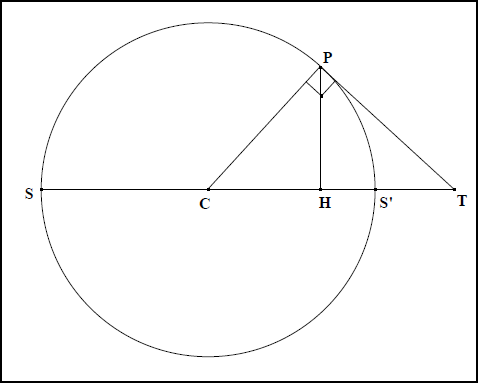
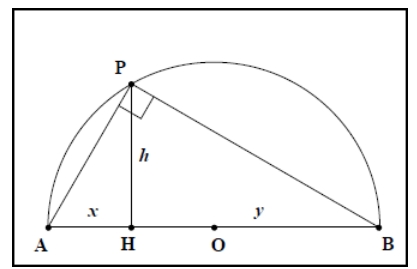
Avec les mêmes notations : Il fonde aussi nombre de ses raisonnements sur deux propriétés implicitement admises, à savoir que le triangle déterminé par trois points sur un cercle dont deux sont les extrémités d’un diamètre est rectangle et que la hauteur issue du sommet de l’angle droit d’un triangle rectangle est moyenne géométrique des longueurs que cette hauteur découpe sur l’hypoténuse (fig. IIa 8).
![]()
Ces propriétés se lisent respectivement à la trente et unième proposition du Livre III des Éléments et en corollaire de la huitième du livre VI. Apollonios les rassemble implicitement en une propriété métrique essentielle du cercle. Elle forme l’arrière plan de son étude sur les coniques et paraît le guider jusque dans l’écriture finale de leurs propriétés métriques.
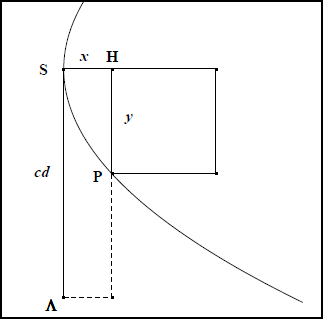
Les propriétés métriques essentielles des coniques sont le sujet de la onzième proposition pour la parabole, puis celui des deux suivantes pour respectivement l’hyperbole et l’ellipse. C’est aussi dans ces trois propositions que ces courbes reçoivent leur nom ; les anciennes dénominations étaient inadaptées au cône oblique et à la manière apollonienne d’obtenir les sections coniques. Le cercle ci-dessus présente la relation métrique qui correspond au cas du cercle. Mutatis mutandis, en imaginant que l’image précédente illustre aussi bien le cas des trois autres courbes, leurs propriétés métriques s’écrivent respectivement :
![]()
Les différentes lettres traduisant les grandeurs suivantes :![]() : distance du sommet au pied de l’ordonnée, notre abscisse.
: distance du sommet au pied de l’ordonnée, notre abscisse.![]() : la distance du point de la conique au pied de l’ordonnée, notre ordonnée.
: la distance du point de la conique au pied de l’ordonnée, notre ordonnée.![]() : le côté droit, en souvenir du latus rectum des traducteurs de la Renaissance.
: le côté droit, en souvenir du latus rectum des traducteurs de la Renaissance.![]() : le côté transverse, en souvenir du latus transversum.
: le côté transverse, en souvenir du latus transversum.
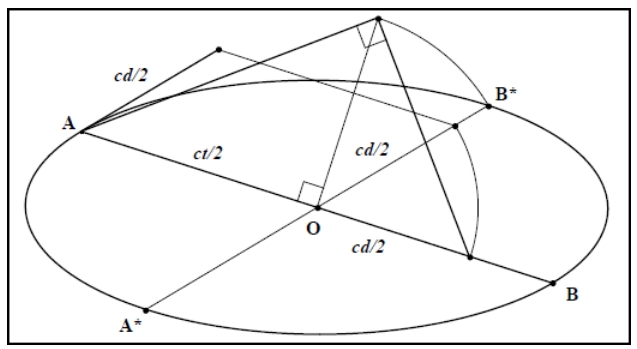
Leur démonstration ne nous satisfait pas complètement, même si la rigueur du l’exposé est indiscutable. Apollonios y fait apparaître le côté droit comme un magicien sortirait un lapin de son chapeau. Nous savons seulement qu’il s’agit d’une quatrième proportionnelle à trois autres grandeurs entièrement déterminées par la donnée du cône et de la section. C’est donc une longueur constante, celle que nous notons ![]() dans les formules. En outre, Apollonios n’utilise pas les mêmes notations entre ces trois propositions pour désigner les mêmes points. Les propriétés métriques des coniques nous apparaissent donc dans des écritures si différentes qu’il nous faut faire un réel effort pour en reconnaître les éléments communs. Ces deux raisons nous ont conduit à rédiger des démonstrations qui restituent une analyse de la question en apportant les éléments de compréhension absents du texte d’Apollonios. La figure IIa 9 expose les éléments de la démonstration.
dans les formules. En outre, Apollonios n’utilise pas les mêmes notations entre ces trois propositions pour désigner les mêmes points. Les propriétés métriques des coniques nous apparaissent donc dans des écritures si différentes qu’il nous faut faire un réel effort pour en reconnaître les éléments communs. Ces deux raisons nous ont conduit à rédiger des démonstrations qui restituent une analyse de la question en apportant les éléments de compréhension absents du texte d’Apollonios. La figure IIa 9 expose les éléments de la démonstration.
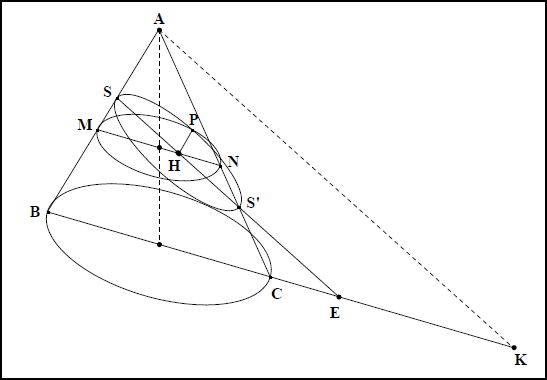
![]() est un triangle passant par l’axe du cône.
est un triangle passant par l’axe du cône.![]() est un diamètre du cercle de base.
est un diamètre du cercle de base.![]() est l’axe de la section conique ;
est l’axe de la section conique ; ![]() et
et ![]() en sont les sommets (le point
en sont les sommets (le point ![]() n’existe pas pour la parabole).
n’existe pas pour la parabole).![]() est la parallèle à l’axe
est la parallèle à l’axe ![]() , passant par le sommet du cône,
, passant par le sommet du cône, ![]() (la droite
(la droite ![]() est une donnée inutile pour la parabole).
est une donnée inutile pour la parabole).![]() est un point de la section.
est un point de la section.![]() est le cercle parallèle à la base et passant par
est le cercle parallèle à la base et passant par ![]() .
.![]() est le pied de la perpendiculaire à (MN), abaissée du point
est le pied de la perpendiculaire à (MN), abaissée du point ![]() .
.
Le dessin comporte beaucoup d’éléments qui n’interviennent pas dans la démonstration. En le simplifiant au maximum, on obtient les schémas suivants pour les différentes sections coniques : fig. IIa 10 pour l’ellipse, fig. IIa 11 pour l’hyperbole, fig. IIa 12 pour la parabole. Dans ces figures, le point ![]() est hors du plan de la figure.
est hors du plan de la figure.
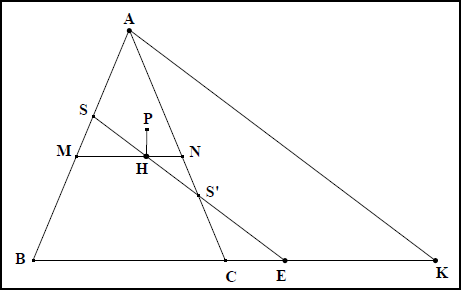
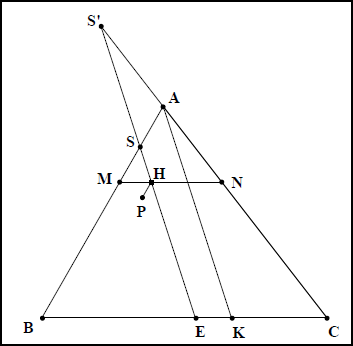
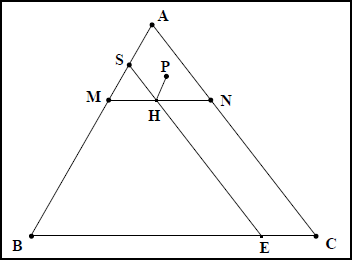
Dans les trois cas de figure, la démonstration s’appuie sur l’identité : ![]() (le cercle
(le cercle ![]() ne sert pas à autre chose). Le but de la démonstration est de substituer aux grandeurs
ne sert pas à autre chose). Le but de la démonstration est de substituer aux grandeurs ![]() et
et ![]() une expression qui fasse intervenir
une expression qui fasse intervenir ![]() et des grandeurs constantes par rapport au point variable
et des grandeurs constantes par rapport au point variable ![]() .
.
Suivons Apollonios en examinant d’abord le cas de la parabole :
![]() , car le cercle
, car le cercle ![]() est parallèle à la base du cône. Et,
est parallèle à la base du cône. Et, ![]() , car la section est une parabole. En conséquence,
, car la section est une parabole. En conséquence, ![]() est un parallélogramme. Donc
est un parallélogramme. Donc ![]() .
.
Grâce à la similitude des triangles ![]() et
et ![]() ,
, ![]() .
.
Grâce à la similitude des triangles ![]() et
et ![]() ,
, ![]() .
.
Substituons ![]() à
à ![]() dans le second rapport,
dans le second rapport, ![]() .
.
En conclusion, ![]() , écriture de la forme
, écriture de la forme ![]() , en posant
, en posant ![]() et
et ![]() . La constante
. La constante ![]() s’appelle le côté droit que nous notons
s’appelle le côté droit que nous notons ![]() .
.
Dans le texte apollonien, le lecteur remarquera que le côté droit n’est pas défini par l’égalité ![]() mais, mutatis mutandis, par la proportion
mais, mutatis mutandis, par la proportion ![]() qui compare des grandeurs homogènes : d’un côté, des longueurs, de l’autre, des surfaces. Dans le cadre de la géométrie grecque, notre écriture est absurde, car elle sous entend un produit entre
qui compare des grandeurs homogènes : d’un côté, des longueurs, de l’autre, des surfaces. Dans le cadre de la géométrie grecque, notre écriture est absurde, car elle sous entend un produit entre ![]() et
et ![]() . Or, pour un Grec, aucun de ces facteurs n’est un nombre : le premier est une longueur et le second un rapport qui, depuis la découverte des irrationnels, n’est plus interprétable comme un nombre de fois. Toute opération entre des êtres mathématiques de nature différente n’aurait donc aucun sens.
. Or, pour un Grec, aucun de ces facteurs n’est un nombre : le premier est une longueur et le second un rapport qui, depuis la découverte des irrationnels, n’est plus interprétable comme un nombre de fois. Toute opération entre des êtres mathématiques de nature différente n’aurait donc aucun sens.
Les cas de l’hyperbole et de l’ellipse conduisent aux mêmes équations qui se déduisent des mêmes similitudes. En nous appuyant sur les schémas ci-dessus et sur la relation ![]() , la démonstration se déroule de la manière suivante :
, la démonstration se déroule de la manière suivante :
Grâce à la similitude des triangles ![]() et
et ![]() ,
, ![]() .
.
Grâce à la similitude des triangles ![]() et
et ![]() ,
, ![]() .
.
En substituant à ![]() et
et ![]() , les expressions déduites de ces deux proportions, l’égalité
, les expressions déduites de ces deux proportions, l’égalité ![]() devient
devient ![]() : (1).
: (1).
Posons ![]() et définissons le côté droit
et définissons le côté droit ![]() par la proportion :
par la proportion :
![]()
![]() existe comme quatrième proportionnelle à trois grandeurs connues.
existe comme quatrième proportionnelle à trois grandeurs connues.
Pour l’hyperbole, (1) s’écrit alors :
![]()
Pour l’ellipse : ![]()
Examinons maintenant la relation (1) du point de vue d’Apollonios en nous aidant de la figure IIa 13. Les lettres ![]() ,
, ![]() ,
, ![]() et
et ![]() présentent les mêmes points que sur le schéma en relation avec l’hyperbole ;
présentent les mêmes points que sur le schéma en relation avec l’hyperbole ; ![]() est défini par la quatrième proportionnelle inconnue dans l’équation
est défini par la quatrième proportionnelle inconnue dans l’équation ![]() . Nous constatons que
. Nous constatons que ![]() , où
, où ![]() est appelé le côté droit ; c’est une grandeur fixe, car définie par la proportion
est appelé le côté droit ; c’est une grandeur fixe, car définie par la proportion ![]() dans laquelle les trois autres grandeurs sont fixes par rapport à
dans laquelle les trois autres grandeurs sont fixes par rapport à ![]() . Remarquons que
. Remarquons que ![]() note le côté transverse.
note le côté transverse.
En raisonnant à la manière d’Apollonios, l’égalité (1) s’écrit sous la forme ![]() .
.
Or, ![]() et
et ![]() . Donc,
. Donc, ![]() . On en déduit l’égalité :
. On en déduit l’égalité : ![]() , c’est-à-dire,
, c’est-à-dire, ![]() .
.
Or, ![]() équivaut à
équivaut à ![]() . En conséquence,
. En conséquence, ![]() .
.
Autrement dit, le carré de l’ordonnée est égal au rectangle sous le côté droit et l’abscisse (![]() ) augmenté du rectangle (
) augmenté du rectangle (![]() ) semblable au rectangle sous le côté droit et le côté transverse (
) semblable au rectangle sous le côté droit et le côté transverse (![]() ).
).
Sans reprendre le déroulement complet de l’explication précédente, examinons le cas de l’ellipse en nous aidant du dessin ci-dessous (fig. IIa 14).
![]() et
et ![]() sont à nouveau définis par
sont à nouveau définis par ![]() et par
et par ![]() ;
; ![]() note toujours le côté droit et
note toujours le côté droit et ![]() le côté transverse.
le côté transverse.
Les proportions ![]() et
et ![]() nous conduisent à nouveau à l’égalité
nous conduisent à nouveau à l’égalité ![]() , c’est-à-dire,
, c’est-à-dire, ![]() .
.
Comme ![]() équivaut à
équivaut à ![]() ,
, ![]() .
.
Autrement dit, le carré de l’ordonnée est égal au rectangle sous le côté droit et l’abscisse (![]() ) diminué du rectangle (
) diminué du rectangle (![]() ) semblable au rectangle sous le côté droit et le côté transverse (
) semblable au rectangle sous le côté droit et le côté transverse (![]() ).
).
Dans l’œuvre d’Apollonios et jusqu’aux mathématiciens français du premier XVIIe siècle, ces trois relations métriques ne seront pas considérées comme une caractéristique de chacune des coniques, pas plus que la relation ![]() pour le cercle. En outre, nous ne connaissons aucune démonstration de leur réciproque qui nous permettrait de penser que les mathématiciens de l’Antiquité les ont envisagées comme des propriétés caractéristiques de leur courbe. Il fallait en effet accepter de considérer les courbes et leur équations comme deux faces d’une même réalité. Ce point de vue, Descartes l’a rendu possible dans sa nouvelle géométrie en faisant passer ces relations du domaine des grandeurs à celui des nombres. Mais si Descartes avait rencontré un Apollonios, ce dernier lui aurait, sans aucun doute, fait remarquer que la géométrie cartésienne ne justifiait qu’un mode de calcul sur les longueurs, qu’elle se fondait sur des constructions bien connues dans l’Antiquité et qu’elle esquivait la question de l’irrationalité.
pour le cercle. En outre, nous ne connaissons aucune démonstration de leur réciproque qui nous permettrait de penser que les mathématiciens de l’Antiquité les ont envisagées comme des propriétés caractéristiques de leur courbe. Il fallait en effet accepter de considérer les courbes et leur équations comme deux faces d’une même réalité. Ce point de vue, Descartes l’a rendu possible dans sa nouvelle géométrie en faisant passer ces relations du domaine des grandeurs à celui des nombres. Mais si Descartes avait rencontré un Apollonios, ce dernier lui aurait, sans aucun doute, fait remarquer que la géométrie cartésienne ne justifiait qu’un mode de calcul sur les longueurs, qu’elle se fondait sur des constructions bien connues dans l’Antiquité et qu’elle esquivait la question de l’irrationalité.
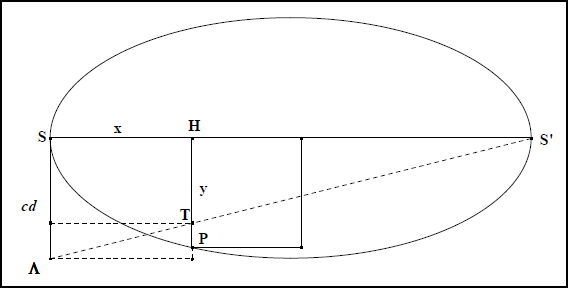
Les figures suivantes visualisent les relations d’Apollonios dans les trois coniques (fig. IIa 15 pour la parabole, fig. IIa 16 pour l’ellipse, fig IIa 17 pour l’hyperbole). Dans ces figures on a noté : ![]() ,
, ![]() ,
, ![]() et
et ![]() . Le point
. Le point ![]() se trouve à l’intersection de
se trouve à l’intersection de ![]() et de l’ordonnée
et de l’ordonnée ![]() .
.
Parabole : le carré sur ![]() est égal au rectangle
est égal au rectangle ![]() ou
ou ![]() .
.
Ellipse : le carré sur ![]() est égal au rectangle
est égal au rectangle ![]() diminué du rectangle
diminué du rectangle ![]() ou
ou ![]() .
.
Hyperbole : le carré sur ![]() est égal au rectangle
est égal au rectangle ![]() augmenté du rectangle
augmenté du rectangle ![]() ou
ou ![]() .
.
Dans le premier livre des Coniques, on trouve d’autres relations métriques qui généralisent aux coniques celles déjà connues sur le cercle. La figure IIa 18 présente, dans le cercle, les éléments concernés : tangente ![]() , ordonnée
, ordonnée ![]() , diamètre
, diamètre ![]() . Le côté droit, que nous notons
. Le côté droit, que nous notons ![]() , n’est pas représenté sur ce dessin. Dans le cas du cercle,
, n’est pas représenté sur ce dessin. Dans le cas du cercle, ![]() et donc
et donc ![]() ; les relations encadrées se simplifient alors en
; les relations encadrées se simplifient alors en ![]() , égalité que nous avons rencontrée dans les calculs précédents, et en
, égalité que nous avons rencontrée dans les calculs précédents, et en ![]() . Les relations sous leur forme générale concernent les trois coniques à centre : cercle, ellipse et hyperbole. La première se lit à la vingt et unième proposition, la seconde, à la trente-septième.
. Les relations sous leur forme générale concernent les trois coniques à centre : cercle, ellipse et hyperbole. La première se lit à la vingt et unième proposition, la seconde, à la trente-septième.
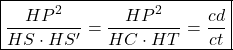
Apollonios traduit la première de ces relations sous une forme qui, en considérant un second point sur la conique, élimine le terme constant ![]() . Notons
. Notons ![]() ce point et notons
ce point et notons ![]() le pied de son ordonnée sur le diamètre. On obtient alors l’égalité
le pied de son ordonnée sur le diamètre. On obtient alors l’égalité ![]() qui répond comme un écho à celle donnée à la vingtième proposition pour la parabole, à savoir
qui répond comme un écho à celle donnée à la vingtième proposition pour la parabole, à savoir ![]() .
.
La seconde égalité ![]() est donnée en même temps que cette autre,
est donnée en même temps que cette autre, ![]() , à la trente-septième proposition. Elles sont utilisées par Apollonios dans les propositions suivantes qui étudient les transformations subies par les relations fondamentales lors « d’un changement de repère ».
, à la trente-septième proposition. Elles sont utilisées par Apollonios dans les propositions suivantes qui étudient les transformations subies par les relations fondamentales lors « d’un changement de repère ».
Apollonios utilise à la trente-quatrième proposition le fait que le conjugué harmonique du pied de l’ordonnée d’un point ![]() par rapport aux sommets d’une conique à centre est le point d’intersection, avec le diamètre, de la tangente issue de
par rapport aux sommets d’une conique à centre est le point d’intersection, avec le diamètre, de la tangente issue de ![]() . Cette relation, que nous écrivons
. Cette relation, que nous écrivons ![]() , était connue au moins pour le cercle, puisque nous pouvons la lire dans les Éléments d’Euclide. La trente-cinquième proposition nous donne l’égalité correspondant au cas de la parabole, à savoir
, était connue au moins pour le cercle, puisque nous pouvons la lire dans les Éléments d’Euclide. La trente-cinquième proposition nous donne l’égalité correspondant au cas de la parabole, à savoir ![]() : la sous tangente, c’est-à-dire, le segment déterminé, sur le diamètre, par l’ordonnée et la tangente d’un point sur la conique, est toujours coupée en deux par le sommet. La question des relations métriques est maintenant résolue pour l’essentiel. Il nous reste à examiner celle relative aux tangentes.
: la sous tangente, c’est-à-dire, le segment déterminé, sur le diamètre, par l’ordonnée et la tangente d’un point sur la conique, est toujours coupée en deux par le sommet. La question des relations métriques est maintenant résolue pour l’essentiel. Il nous reste à examiner celle relative aux tangentes.
Nous ne savons pas quelle fut l’étendue de la notion de tangente avant Apollonios. La seule définition explicite que l’histoire nous ait transmis se lit au troisième livre des Éléments d’Euclide et concerne exclusivement le cercle. Dans ces définitions, « toucher » signifie « passer par un point » : « Une droite est tangente à un cercle si elle touche le cercle mais, prolongée, ne le traverse pas », « sont tangents, les cercles qui se touchent sans se couper ». Dans le premier livre des Coniques, au vu des démonstrations qui traitent du cas des tangentes, nous pourrions penser qu’Apollonios s’est appuyé sur la définition euclidienne en l’étendant aux coniques non circulaires. Il y démontre, en effet, comme le fait Euclide pour le cercle, que certaine droite touchant la courbe en un point et respectant des conditions qui nous assurent de son existence, reste à l’extérieur de la courbe, et que, suivant toujours Euclide, cette droite est unique. Cette définition est suffisante pour considérer des tangentes à une conique mais celles des cercles tangents ne convient pas pour traiter, comme dans le quatrième livre, le cas de coniques tangentes entre elles, car deux coniques tangentes en un point se recoupent en général. Nous ne savons qui fut le premier à lever la difficulté mais la lecture du quatrième livre nous montre que les Grecs avaient compris le caractère local de la notion de tangente, car Apollonios y considère implicitement que deux coniques sont tangentes, lorsqu’elle partagent la même tangente au point de contact. L’absence d’une définition explicite corrigeant la définition euclidienne laisse à penser que la question fut examinée avant la rédaction des Coniques.
Nous avons dit plus haut comment Apollonios a traité les cas des droites tangentes à une conique. Cette question mérite quelques explications supplémentaires, car la démarche apollonienne diffère de la nôtre en ce sens qu’il nous semble parfois prendre le problème à l’envers. La cause réside dans la définition euclidienne qui ne permet pas d’assurer à priori l’existence d’une droite touchant une section, c’est-à-dire, passant par un point mais demeurant à l’extérieur de la section. La démarche moderne est tout autre, car nous faisons reposer l’existence d’une tangente sur la dérivabilité de la fonction qui représente la courbe étudiée. La différence entre ces deux points de vue est déjà claire pour la tangente au cercle. Nous savons, en effet, que la tangente en un point de la circonférence d’un cercle est perpendiculaire à la droite déterminée par le point de contact et le centre du cercle. De nos jours, une présentation possible de cette propriété suivrait de préférence la démarche suivante :
la circonférence d’un cercle est localement la représentation graphique d’une fonction dérivable
![]()
en un point de la circonférence, il existe toujours une tangente, unique par définition de la dérivée
![]()
la droite joignant le point de contact et le centre du cercle est perpendiculaire à la tangente
Euclide, contraint par sa propre définition, commence par la propriété relative à l’angle entre la tangente et le rayon. Elle lui assure l’existence d’une droite touchant la circonférence en restant à l’extérieur du cercle. En un point de la circonférence :
il existe une droite perpendiculaire à celle joignant le point considéré au centre du cercle
![]()
cette perpendiculaire prolongée ne recoupe pas le cercle
![]()
cette perpendiculaire est une tangente et elle est unique
On va retrouver la même démarche chez Apollonios dans les propositions 33 à 37, dont nous avons déjà parlé dans le paragraphe sur les relations métriques : Apollonios démontre tout d’abord que la droite issue d’un point de la section et déterminée par la donnée d’un second point qui, sur le diamètre, vérifie certaines relations métriques est une tangente. Étant maintenant assuré de l’existence des tangentes, il peut les envisager comme des données. Il démontre donc, ensuite, en une réciproque que nous aurions considérée en premier, que la tangente donnée coupe le diamètre en un point qui satisfait aux relations métriques précédentes. La boucle est bouclée.
Avec la question des tangentes, se clôt ce bref commentaire dont l’ambition fut non pas de proposer un exposé détaillé des résultats du premier livre mais de discuter autour des éléments fondamentaux qui conduisent à l’ensemble de ses résultats. Cette raison impose l’abandon de deux sujets importants mais qui dérivent des relations métriques revues dans ce commentaire : celui sur les hyperboles conjuguées ou, à la fin du livre, celui sur les calculs qui conduisent au « changement de repère ».
Résumé du Livre II des Coniques d'Apollonios
Le Livre II ne considère plus les coniques dans l’espace mais comme des figures planes ayant des propriétés métriques caractéristiques. Il est consacré d’une part aux propriétés des asymptotes aux hyperboles, et d’autre part aux constructions des diamètres, axes, centres et tangentes à des coniques données. Le Livre II utilise essentiellement les relations entre ordonnées et abscisses, exposées aux propositions 11, 12, 13, 20 et 21 du Livre I. On a vu, dans notre commentaire du Livre I, que ces relations correspondent aux écritures suivantes, où ![]() désigne le côté droit ou paramètre, et
désigne le côté droit ou paramètre, et ![]() le côté transverse ou diamètre :
le côté transverse ou diamètre :
pour la parabole : ![]() ;
;
pour l’hyperbole : ![]() ou
ou ![]() ;
;
pour l’ellipse : ![]() ou
ou ![]() .
.
La caractérisation du pied de la tangente comme conjugué harmonique du pied de l’ordonnée par rapport aux sommets est une autre propriété très usitée dans le Livre II. On la trouve dans les propositions 33, 34, 35, 36, 37 du Livre I et elle se traduit actuellement dans les écritures suivantes, où ![]() désigne l’abscisse du pied de la tangente sur le diamètre :
désigne l’abscisse du pied de la tangente sur le diamètre :
pour la parabole : ![]() ;
;
pour l’hyperbole, l’ellipse ou le cercle : ![]() ou
ou ![]() .
.
Un grand nombre de propositions du Livre II utilise les propositions 46 à 51 du Livre I. Celles-ci permettent la découverte de nouveaux diamètres et ordonnées et la transformation correspondante des propriétés caractéristiques associées. Elles permettent de plus l’étude des hyperboles opposées (les deux branches de notre hyperbole) et des hyperboles conjuguées. Ces dernières ont été définies, à la soixantième et dernière proposition du Livre I : si on a une hyperbole de côté droit ![]() et de côté transverse
et de côté transverse ![]() , alors l’hyperbole conjuguée a le même centre, échange ses abscisses et ordonnées avec l’hyperbole initiale, et possède un côté droit
, alors l’hyperbole conjuguée a le même centre, échange ses abscisses et ordonnées avec l’hyperbole initiale, et possède un côté droit ![]() et un côté transverse
et un côté transverse ![]() tels que :
tels que : ![]() et
et ![]() .
.
Le Livre II s’ouvre sur la définition d’une asymptote. Il s’agit d’une droite qui, conformément à l’étymologie, ne rencontre pas l’hyperbole. Elle passe par le centre et par un point situé sur la tangente au sommet d’un diamètre. Le carré de la distance de ce point au sommet est égal au quart de la « figure » (c’est-à-dire ![]() ). Les propositions suivantes démontrent que de telles droites ne rencontrent pas l’hyperbole, et que ce sont les meilleures possibles : au sens où toute droite issue du centre et comprise dans l’angle intérieur des asymptotes rencontre l’hyperbole. En outre les asymptotes sont les mêmes quel que soit le sommet choisi sur l’hyperbole. Apollonios décrit ensuite les propriétés des segments découpés sur une sécante par la courbe et les asymptotes : symétrie des asymptotes par rapport au diamètre, constance du produit des distances d’un point de la courbe aux asymptotes (c’est encore le quart de la figure). De même le produit des distances d’un point de l’hyperbole aux asymptotes sous deux directions données est constant.
). Les propositions suivantes démontrent que de telles droites ne rencontrent pas l’hyperbole, et que ce sont les meilleures possibles : au sens où toute droite issue du centre et comprise dans l’angle intérieur des asymptotes rencontre l’hyperbole. En outre les asymptotes sont les mêmes quel que soit le sommet choisi sur l’hyperbole. Apollonios décrit ensuite les propriétés des segments découpés sur une sécante par la courbe et les asymptotes : symétrie des asymptotes par rapport au diamètre, constance du produit des distances d’un point de la courbe aux asymptotes (c’est encore le quart de la figure). De même le produit des distances d’un point de l’hyperbole aux asymptotes sous deux directions données est constant.
La figure IIb 1 et les égalités ci-dessous résument ces différentes propriétés.
Livre I :
![]() (prop. 12) ;
(prop. 12) ;
![]() (prop. 21).
(prop. 21).
Livre II :
![]() (prop. 1 et 22) ;
(prop. 1 et 22) ;
![]() (prop. 8) ;
(prop. 8) ;
![]() (prop. 10) ;
(prop. 10) ;
![]() (prop. 11) ;
(prop. 11) ;
![]() (prop. 16) ;
(prop. 16) ;
![]() (prop. 19) ;
(prop. 19) ;
![]() (prop. 23).
(prop. 23).
Avec ces propriétés, Apollonios démontre que la distance entre l’hyperbole et ses asymptotes peut être rendue plus petite que tout intervalle donné (proposition 14), ce que nous énoncerions : la distance entre l’hyperbole et ses asymptotes tend vers zéro. Cette proposition, l’une des rares de nature infinitésimale dans la géométrie grecque classique, n’est pas utilisée ailleurs dans le Livre II. Elle permet simplement de conclure que les asymptotes sont les droites les plus proches de l’hyperbole parmi celles qui ne la coupent pas.
Apollonios démontre ensuite (propositions 15 et 17) que ces asymptotes sont aussi celles de l’hyperbole opposée (l’autre branche de l’hyperbole) et celles des hyperboles conjuguées. La proposition 20 démontre que la définition (donnée plus haut) des hyperboles conjuguées ne dépend pas du diamètre choisi initialement.
Le groupe de propositions qui suit porte sur la situation des points d’intersection de deux tangentes ou de deux sécantes à diverses coniques. Les énoncés de ces propositions sont relativement simples mais les démonstrations, comme toutes celles de ce type dans la géométrie grecque, semblent liées à la considération de la figure. Apollonios démontre que dans la parabole, ou dans l’hyperbole, deux sécantes, dont les points de rencontre avec la conique ne s’entourent pas, se rencontrent à l’extérieur de la courbe (propositions 24 et 25). La figure IIb 2 illustre le cas de l’hyperbole quand les points ne s’entourent pas et la figure IIb 3 présente la situation où les points s’entourent.
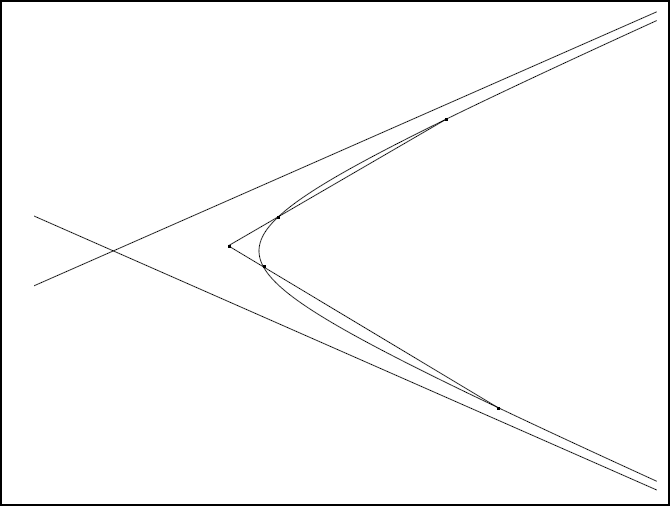
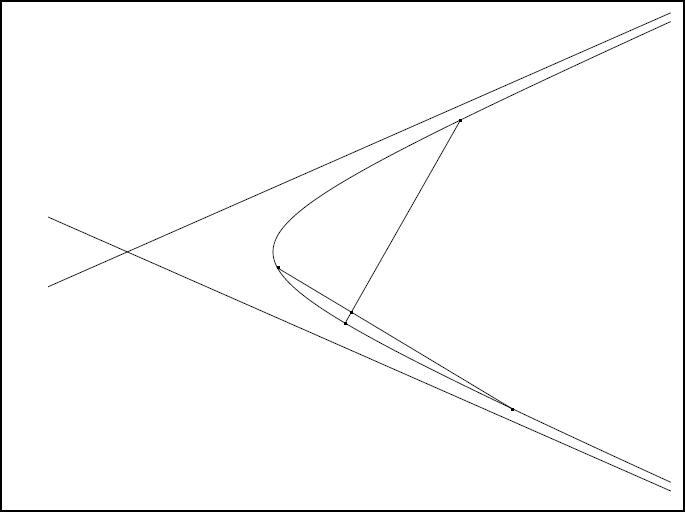
De même, deux tangentes à une ellipse sont soit parallèles soit sécantes du même côté que le centre par rapport à la droite joignant les points de contact (proposition 27). On a le même résultat pour l’hyperbole en considérant deux tangentes respectivement à chacune des branches opposées (proposition 31).
Enfin, on trouve dans ce Livre II un ensemble de résultats concernant les diamètres des coniques et leur construction à partir de sécantes ou de tangentes. Ainsi le parallélisme de la tangente au sommet avec la direction de la symétrie oblique par rapport au diamètre est plusieurs fois utilisé, ainsi que sa réciproque. Ceci permet de définir un diamètre comme l’ensemble des milieux de sécantes parallèles (propositions 28, 34, 36), et comme la droite joignant l’intersection de deux tangentes avec le milieu des points de contact (propositions 29, 30, 38, 39, 40). Ces propriétés sont démontrées pour toutes les coniques, et pour les deux branches d’une même hyperbole. Elles permettent aussi la construction des diamètres conjugués.
Le livre II s’achève sur d’autres problèmes de construction : trouver les diamètres, le centre, l’axe d’une conique donnée. Un diamètre est déterminé par les milieux de deux sécantes parallèles (proposition 44) ; le centre par l’intersection de deux diamètres déjà tracés (proposition 45) ; l’axe d’une parabole par un diamètre quelconque, une sécante perpendiculaire à ce diamètre : l’axe est parallèle au diamètre et passe par le milieu de la sécante perpendiculaire (proposition 46) ; l’axe d’une ellipse ou d’une hyperbole est déterminé par la médiatrice d’une corde joignant deux points à égale distance du centre (proposition 47).
Puis, la conique étant toujours donnée, il s’agit de tracer une tangente issue d’un point extérieur, et une tangente faisant un angle donné avec un diamètre. Cette dernière propriété revient à trouver dans une conique deux diamètres conjugués dont on donne l’angle. Apollonios donne les conditions, en particulier pour l’ellipse, que doit vérifier cet angle. La tangente issue d’un point extérieur est obtenue en faisant passer un diamètre par ce point et en en prenant le conjugué harmonique par rapport aux sommets. Cela donne le pied de l’ordonnée, dont la direction est la tangente au sommet (proposition 49).
Interprétation moderne des relations d’Apollonios
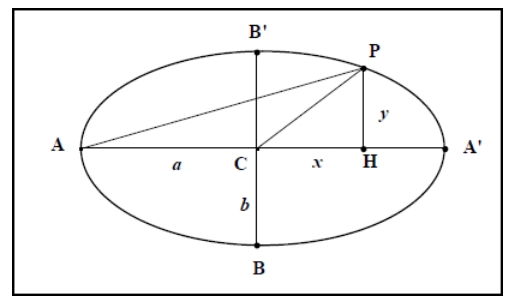
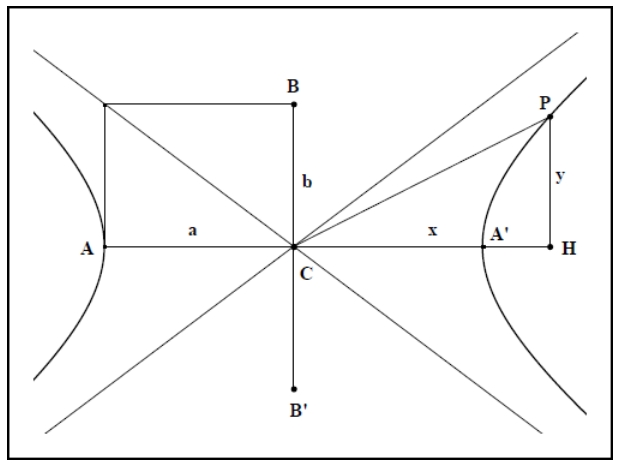
L’étude des coniques se réduit maintenant à un savoir minimum. Les coniques à centre, en particulier, sont systématiquement étudiées dans le repère orthogonal défini sur l’axe focal avec le centre comme origine. Des calculs élémentaires établissent que les coordonnées ![]() repérant un point d’une ellipse ou d’une hyperbole satisfont les équations
repérant un point d’une ellipse ou d’une hyperbole satisfont les équations ![]() ou
ou ![]() . On sait aussi interpréter les nombres figurant aux dénominateurs. Le «
. On sait aussi interpréter les nombres figurant aux dénominateurs. Le « ![]() » mesure le demi-axe focal ; le «
» mesure le demi-axe focal ; le « ![]() » mesure le petit axe de l’ellipse ou s’il s’agit d’une hyperbole, le segment de tangente allant du sommet de l’axe jusqu’au point de sa rencontre avec l’une des asymptotes. Tous ces éléments sont placés sur les figures (voir fig. IIc 1 pour l’ellipse et fig. IIc 2 pour l’hyperbole).
» mesure le petit axe de l’ellipse ou s’il s’agit d’une hyperbole, le segment de tangente allant du sommet de l’axe jusqu’au point de sa rencontre avec l’une des asymptotes. Tous ces éléments sont placés sur les figures (voir fig. IIc 1 pour l’ellipse et fig. IIc 2 pour l’hyperbole).
Une expression des constantes ![]() et
et ![]() en fonction des constantes apolloniennes
en fonction des constantes apolloniennes ![]() et
et ![]() est possible non seulement pour ce repère orthogonal, mais aussi pour tous les repères reposant sur les axes employés par Apollonios, c’est-à-dire, pour les repères dont les axes sont construits sur un diamètre et sur la tangente à l’un de ses sommets. Le qualificatif d’apollonien permet de distinguer ces repères et de simplifier le discours. Néanmoins, le lecteur gardera à l’esprit qu’il s’agit là d’un anachronisme commode, car le concept de repère n’appartient pas à l’époque d’Apollonios. Une translation d’un repère apollonien au centre de la conique, donne une repère formé sur les diamètres conjugués en raison du parallélisme de la tangente et du diamètre conjugué qui est aussi le second diamètre de l’ellipse. Le texte suivant se propose de montrer que la forme des équations réduites se maintient dans tout repère formé de deux diamètres conjugués. Auparavant, il se propose d’établir les relations entre les constantes «
est possible non seulement pour ce repère orthogonal, mais aussi pour tous les repères reposant sur les axes employés par Apollonios, c’est-à-dire, pour les repères dont les axes sont construits sur un diamètre et sur la tangente à l’un de ses sommets. Le qualificatif d’apollonien permet de distinguer ces repères et de simplifier le discours. Néanmoins, le lecteur gardera à l’esprit qu’il s’agit là d’un anachronisme commode, car le concept de repère n’appartient pas à l’époque d’Apollonios. Une translation d’un repère apollonien au centre de la conique, donne une repère formé sur les diamètres conjugués en raison du parallélisme de la tangente et du diamètre conjugué qui est aussi le second diamètre de l’ellipse. Le texte suivant se propose de montrer que la forme des équations réduites se maintient dans tout repère formé de deux diamètres conjugués. Auparavant, il se propose d’établir les relations entre les constantes « ![]() » et «
» et « ![]() », augmentées de quelques autres, et les constantes apolloniennes
», augmentées de quelques autres, et les constantes apolloniennes ![]() et
et ![]() et de montrer qu’elles sont indépendantes du repère formé sur deux axes conjugués.
et de montrer qu’elles sont indépendantes du repère formé sur deux axes conjugués.
Établir les relations entre les différentes constantes suppose que les équations réduites existent dans tout repère formé de deux diamètres conjugués. Sous cette hypothèse, l’entreprise n’est pas très difficile et se réduit à un simple jeu d’écriture. Elle repose sur la transformation de l’équation apollonienne lors d’une translation, au centre de la conique, du repère apollonien, construit sur le diamètre ![]() et sur la tangente au sommet
et sur la tangente au sommet ![]() . Les éléments de la démonstration sont représentés sur les figures. Laissons de côté l’hyperbole qui nous mènerait à une répétition des arguments et considérons seulement l’ellipse. Les coordonnées d’un point courant
. Les éléments de la démonstration sont représentés sur les figures. Laissons de côté l’hyperbole qui nous mènerait à une répétition des arguments et considérons seulement l’ellipse. Les coordonnées d’un point courant ![]() forment le couple
forment le couple ![]() dans le repère apollonien et le couple
dans le repère apollonien et le couple ![]() dans le repère utilisant le même jeu d’axes mais rapporté au centre, autrement dit dans le repère formé de deux diamètres conjugués.
dans le repère utilisant le même jeu d’axes mais rapporté au centre, autrement dit dans le repère formé de deux diamètres conjugués.
Dans le premier repère, l’équation d’Apollonios s’écrit ![]() .
.
D’où, ![]() .
.
En utilisant, l’égalité ![]() , il vient
, il vient
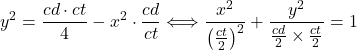
Par identification avec ![]() , on obtient
, on obtient ![]() et
et ![]() .
.
D’où, ![]() (on le savait déjà) et
(on le savait déjà) et ![]() .
.
En formant la proportion ![]() , la dernière égalité induit une construction simple de
, la dernière égalité induit une construction simple de ![]() .
.
Sur la figure IIc 3, le côté droit est reporté sur la tangente au sommet. Apollonios aurait choisi de le reporter sur une perpendiculaire au diamètre en l’un de ses sommets pour former un vrai rectangle de dimensions ![]() et
et ![]() , ou, en termes apolloniens, il forme le rectangle
, ou, en termes apolloniens, il forme le rectangle ![]() en tant que surface qu’il compare à la surface carrée
en tant que surface qu’il compare à la surface carrée ![]() . La découverte de rapports irrationnels lui interdisait de passer d’une comparaison toujours licite entre des grandeurs géométriques à celle des nombres censés les mesurer, comme
. La découverte de rapports irrationnels lui interdisait de passer d’une comparaison toujours licite entre des grandeurs géométriques à celle des nombres censés les mesurer, comme ![]() fois
fois ![]() et
et ![]() .
.
Par ailleurs, l’égalité ![]() permet une expression de l’excentricité
permet une expression de l’excentricité ![]() d’une conique à centre en fonction des nombres
d’une conique à centre en fonction des nombres![]() et
et ![]() .
.
En effet, dans le cas de l’ellipse : ![]() .
.
Dans le cas de l’hyperbole : ![]() .
.
Le cas de la parabole est plus simple. Son équation réduite dans un repère orthonormé porté par l’axe et la tangente au sommet est de la forme ![]() . Donc,
. Donc, ![]() . Comme
. Comme ![]() $ est le double de la distance focale
$ est le double de la distance focale ![]() dans ce repère, nous avons aussi
dans ce repère, nous avons aussi ![]() .
.
Dans un repère apollonien, seule l’égalité ![]() se conserve.
se conserve.
Constructions simples du côté droit
Le paragraphe précédent a montré comment passer des grandeurs apolloniennes ![]() et
et ![]() aux constantes apparaissant dans les équations modernes. Celui-ci se propose de représenter le côté droit à partir des grandeurs données dans le texte d’Apollonios, donc, indépendamment des équations réduites modernes. Le dessin du côté transverse ne posant pas de difficulté, la suite ne concerne que celui du côté droit. La construction proposée s’appuie sur celle de la moyenne géométrique. La figure IIc 4 illustre la construction de l’égalité
aux constantes apparaissant dans les équations modernes. Celui-ci se propose de représenter le côté droit à partir des grandeurs données dans le texte d’Apollonios, donc, indépendamment des équations réduites modernes. Le dessin du côté transverse ne posant pas de difficulté, la suite ne concerne que celui du côté droit. La construction proposée s’appuie sur celle de la moyenne géométrique. La figure IIc 4 illustre la construction de l’égalité ![]() . En fait, il faut y voir deux constructions, l’une ayant la moyenne géométrique
. En fait, il faut y voir deux constructions, l’une ayant la moyenne géométrique ![]() pour inconnue, l’autre, l’un des facteurs
pour inconnue, l’autre, l’un des facteurs ![]() ou
ou ![]() . Dans la situation où l’inconnue est
. Dans la situation où l’inconnue est ![]() , le cercle de diamètre
, le cercle de diamètre ![]() intercepte la perpendiculaire
intercepte la perpendiculaire ![]() en
en ![]() et nous donne
et nous donne ![]() . Dans celle où
. Dans celle où ![]() et
et ![]() sont connues, c’est la perpendiculaire
sont connues, c’est la perpendiculaire ![]() à l’hypoténuse qui nous donne
à l’hypoténuse qui nous donne ![]() et le cercle est inutile. La représentation du côté droit demande seulement de connaître la dernière construction.
et le cercle est inutile. La représentation du côté droit demande seulement de connaître la dernière construction.
Au préalable, rapportons les coordonnées d’un point du plan au repère construit sur un axe et sur la tangente à un sommet. Un point de la conique voit donc ses coordonnées satisfaire aux égalités apolloniennes ![]() pour une l’ellipse et
pour une l’ellipse et ![]() pour une l’hyperbole. En particulier, les points de l’ellipse dont l’abscisse est
pour une l’hyperbole. En particulier, les points de l’ellipse dont l’abscisse est ![]() , c’est-à-dire, les deux sommets du second diamètre, ont leurs coordonnées
, c’est-à-dire, les deux sommets du second diamètre, ont leurs coordonnées ![]() qui vérifient l’égalité :
qui vérifient l’égalité :
![]()
C’est une moyenne géométrique. De même, les points de l’hyperbole dont l’abscisse est ![]() ont leurs coordonnées
ont leurs coordonnées ![]() qui vérifient l’égalité
qui vérifient l’égalité ![]() . C’est une autre moyenne géométrique.
. C’est une autre moyenne géométrique.
Dans l’ellipse, ![]() et
et ![]() sont connus. En reportant
sont connus. En reportant ![]() sur la perpendiculaire, en
sur la perpendiculaire, en ![]() , au diamètre
, au diamètre ![]() , la construction de la moyenne géométrique détermine le demi-côté droit sur
, la construction de la moyenne géométrique détermine le demi-côté droit sur ![]() . Un cercle de centre
. Un cercle de centre ![]() reporte le côté droit sur le diamètre conjugué et deux parallèles suffiraient à le reporter sur la tangente au sommet (voir figure IIc 5).
reporte le côté droit sur le diamètre conjugué et deux parallèles suffiraient à le reporter sur la tangente au sommet (voir figure IIc 5).
Dans l’hyperbole, ![]() et
et ![]() sont connus, l’un comme symétrique de
sont connus, l’un comme symétrique de ![]() par rapport à
par rapport à ![]() , l’autre en traçant la parallèle à la tangente au sommet. En reportant
, l’autre en traçant la parallèle à la tangente au sommet. En reportant ![]() sur la perpendiculaire, en
sur la perpendiculaire, en ![]() , au diamètre
, au diamètre ![]() , la construction de la moyenne géométrique détermine le demi-côté droit sur
, la construction de la moyenne géométrique détermine le demi-côté droit sur ![]() comme pour l’ellipse. Le côté droit se reporte ensuite sur l’ordonnée
comme pour l’ellipse. Le côté droit se reporte ensuite sur l’ordonnée ![]() , puis, à l’aide d’une parallèle au diamètre sur la tangente au sommet (voir fig. IIc 6).
, puis, à l’aide d’une parallèle au diamètre sur la tangente au sommet (voir fig. IIc 6).
La représentation du côté droit sur la figure d’une parabole procède d’une construction entièrement différente bien que le repère soit toujours formé d’un diamètre et de la tangente en son sommet. Les coordonnées d’un point courant sur la courbe satisfont donc à l’équation apollonienne ![]() et l’ordonnée du point d’abscisse
et l’ordonnée du point d’abscisse ![]() vérifie l’égalité
vérifie l’égalité ![]() . C’est toujours une moyenne géométrique mais sans grandeur connue à priori. Un changement de méthode s’impose et l’égalité
. C’est toujours une moyenne géométrique mais sans grandeur connue à priori. Un changement de méthode s’impose et l’égalité ![]() suggère la construction d’un losange. Toute ordonnée étant parallèle à la tangente au sommet, une bissectrice de l’angle formé par la tangente au sommet et le diamètre rencontre la courbe en un point
suggère la construction d’un losange. Toute ordonnée étant parallèle à la tangente au sommet, une bissectrice de l’angle formé par la tangente au sommet et le diamètre rencontre la courbe en un point ![]() qui avec le sommet
qui avec le sommet ![]() forme un losange dont les côtés ont même longueur que le côté droit (cf fig. IIc 7).
forme un losange dont les côtés ont même longueur que le côté droit (cf fig. IIc 7).
Stabilité des équations réduites
La première partie de ce texte a montré les relations existant entre les constantes d’Apollonios ![]() et
et ![]() et les nôtres. L’argumentation reposait sur le fait que les égalités
et les nôtres. L’argumentation reposait sur le fait que les égalités ![]() et
et ![]() reliant les coordonnées
reliant les coordonnées ![]() d’un point d’une conique à centre, ont la propriété d’exister dans tout repère formé par deux axes conjugués. Ce paragraphe propose une démonstration de cette propriété en s’appuyant sur la proposition 21 du livre I dont les résultats sont une généralisation aux cas de l’ellipse et de l’hyperbole de la propriété métrique fondamentale du cercle, à savoir,
d’un point d’une conique à centre, ont la propriété d’exister dans tout repère formé par deux axes conjugués. Ce paragraphe propose une démonstration de cette propriété en s’appuyant sur la proposition 21 du livre I dont les résultats sont une généralisation aux cas de l’ellipse et de l’hyperbole de la propriété métrique fondamentale du cercle, à savoir, ![]() . Les égalités numérotées (1) et (2) résument sous une forme moderne ceux qui concernent l’ellipse. Cette démonstration s’accompagne aussi d’un dessin définissant les différents éléments de l’argumentation (voir fig IIc 8).
. Les égalités numérotées (1) et (2) résument sous une forme moderne ceux qui concernent l’ellipse. Cette démonstration s’accompagne aussi d’un dessin définissant les différents éléments de l’argumentation (voir fig IIc 8).
![]()
![]()
Le point ![]() formant le quatrième sommet d’un parallélogramme, nous obtenons les égalités suivantes :
formant le quatrième sommet d’un parallélogramme, nous obtenons les égalités suivantes :
![]() .
.
Soit ![]() .
.
Ou encore : ![]() , car
, car ![]() .
.
C’est-à-dire : ![]() , car
, car ![]() .
.
Soit : ![]() .
.
Ou : ![]() .
.
Soit : ![]() , d’après l’égalité (1) car
, d’après l’égalité (1) car ![]() .
.
Et finalement : ![]() , c’est-à-dire,
, c’est-à-dire, ![]() .
.
Ce résultat est prouvé à partir de ![]() et en utilisant l’égalité (1). Il pourrait se démontrer en partant de
et en utilisant l’égalité (1). Il pourrait se démontrer en partant de ![]() . Le raisonnement conserverait les mêmes articulations mais il considérerait les grandeurs de l’axe conjugué
. Le raisonnement conserverait les mêmes articulations mais il considérerait les grandeurs de l’axe conjugué ![]() et l’égalité (2) se substituerait à l’égalité (1). Le lecteur pourra observer que la relation
et l’égalité (2) se substituerait à l’égalité (1). Le lecteur pourra observer que la relation ![]() fait jouer un rôle parfaitement symétrique aux deux axes. Celui des abscisses est donc arbitraire et pourrait ne pas être le grand axe.
fait jouer un rôle parfaitement symétrique aux deux axes. Celui des abscisses est donc arbitraire et pourrait ne pas être le grand axe.
La stabilité des équations réduites liant les coordonnées d’un point d’une ellipse est maintenant démontrée dans tous les repères formés de deux diamètres conjugués. Le même résultat existe pour l’hyperbole et il se démontre de la même manière, mais en utilisant les relations de la proposition 21 qui, sous une forme moderne, se résument dans les égalités (1′) et (2′). Comme pour l’ellipse, le dessin annexe définit les autres éléments de la démonstration (cf. fig. IIc 9).
![]() (1′)
(1′)
![]() (2′)
(2′)
Le raisonnement est en tout point identique au précédent, mais les propositions (1′) et (2′) entraînent que :
![]() et donc, que :
et donc, que :
![]() .
.
Le diamètre conjugué dans l’hyperbole
Le diamètre conjugué au côté transverse joue donc un rôle important dans l’étude des coniques. Nous avons choisi de le noter ![]() pour traduire l’expression côté transverse conjugué. Il est aussi, dans l’hyperbole comme dans l’ellipse, la longueur que, dans les équations réduites
pour traduire l’expression côté transverse conjugué. Il est aussi, dans l’hyperbole comme dans l’ellipse, la longueur que, dans les équations réduites ![]() et
et ![]() , nous notons
, nous notons ![]() . Toutefois, le diamètre conjugué
. Toutefois, le diamètre conjugué ![]() n’a pas toujours sur la figure d’une hyperbole l’évidence qu’il a sur celle d’une ellipse. Il se voit bien quand les asymptotes sont données, car, en venant couper la tangente à l’un des sommets de l’axe, elles interceptent un segment de la longueur du diamètre conjugué. Sans les asymptotes, le diamètre conjugué n’est plus repérable. Il peut se construire à l’aide de la définition donnée par Apollonios, à savoir l’égalité
n’a pas toujours sur la figure d’une hyperbole l’évidence qu’il a sur celle d’une ellipse. Il se voit bien quand les asymptotes sont données, car, en venant couper la tangente à l’un des sommets de l’axe, elles interceptent un segment de la longueur du diamètre conjugué. Sans les asymptotes, le diamètre conjugué n’est plus repérable. Il peut se construire à l’aide de la définition donnée par Apollonios, à savoir l’égalité ![]() de laquelle, puisque
de laquelle, puisque ![]() , on déduit l’égalité
, on déduit l’égalité ![]() . Sa construction est donc à nouveau celle d’une moyenne géométrique.
. Sa construction est donc à nouveau celle d’une moyenne géométrique.
Le texte suivant et la figure qui l’accompagne en proposent une construction sur la tangente au sommet ![]() , quand les grandeurs connues sont le côté droit
, quand les grandeurs connues sont le côté droit ![]() et le côté transverse
et le côté transverse ![]() (cf. fig IIc 10).
(cf. fig IIc 10).
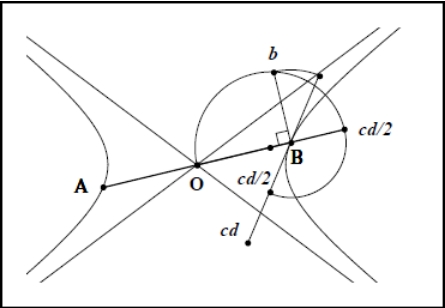
À partir du sommet ![]() , un arc de cercle reporte la longueur
, un arc de cercle reporte la longueur ![]() sur le grand axe, puis le cercle de diamètre
sur le grand axe, puis le cercle de diamètre ![]() intercepte la perpendiculaire réalisant la moyenne géométrique de
intercepte la perpendiculaire réalisant la moyenne géométrique de ![]() et de
et de ![]() , c’est-à-dire, en un point distant de
, c’est-à-dire, en un point distant de ![]() du sommet
du sommet ![]() . Un arc de cercle reporte symétriquement la longueur
. Un arc de cercle reporte symétriquement la longueur ![]() sur la tangente au sommet. En plus de la longueur
sur la tangente au sommet. En plus de la longueur ![]() , ces deux points et le centre nous donnent les deux asymptotes.
, ces deux points et le centre nous donnent les deux asymptotes.
Résumé
Pour la lecture et la compréhension du texte d’Apollonios, aucun des résultats précédents n’est vraiment nécessaire car l’étude faite par Apollonios se suffit à elle-même. Ils ne sont donnés que pour jeter un pont entre la manière moderne de voir les coniques et celle d’Apollonios, et afin de ne pas se sentir trop ignorant à la lecture d’énoncés formulant une mathématique d’un autre temps.
La suite propose un résumé des propriétés précédentes et de quelques autres. L’ensemble pouvant former un vade-mecum du lecteur d’Apollonios.
Les grandeurs ![]() et
et ![]() , des équations
, des équations ![]() et
et ![]() , l’excentricité
, l’excentricité ![]() et la distance focale
et la distance focale ![]() sont reliés au côté droit
sont reliés au côté droit ![]() et au côté transverse
et au côté transverse ![]() par les égalités suivantes :
par les égalités suivantes :
 ;
; pour la parabole. Lorsque le diamètre est l’axe focal,
pour la parabole. Lorsque le diamètre est l’axe focal,  ;
; pour les coniques à centre. Lorsque le diamètre est l’axe focal, la longueur
pour les coniques à centre. Lorsque le diamètre est l’axe focal, la longueur 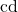 est aussi la distance entre les deux points de la courbe, symétriques par rapport au même foyer. Ainsi, la connaissance de l’une des grandeurs
est aussi la distance entre les deux points de la courbe, symétriques par rapport au même foyer. Ainsi, la connaissance de l’une des grandeurs 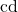 ou
ou  permet la construction de l’autre ;
permet la construction de l’autre ; .
.
La distance ![]() des foyers au centre d’une conique vérifie les égalités
des foyers au centre d’une conique vérifie les égalités ![]() pour l’hyperbole et
pour l’hyperbole et ![]() pour l’ellipse et pour ces deux coniques, les foyers sont les points dont l’ordonnée relative à l’axe focal mesure
pour l’ellipse et pour ces deux coniques, les foyers sont les points dont l’ordonnée relative à l’axe focal mesure ![]() .
.
Le quadruple de la distance focale d’une parabole est déterminée par l’abscisse d’un point commun à la courbe et à une bissectrice de l’angle que forment l’axe focal et la tangente au sommet. Cette abscisse valant ![]() , la distance focale vaut
, la distance focale vaut ![]() .
.
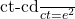 pour l’ellipse, où 0 <
pour l’ellipse, où 0 <  < 1 ;
< 1 ;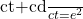 pour l’hyperbole, où
pour l’hyperbole, où  > 1 ;
> 1 ;- pour la parabole,
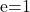 .
.
La directrice d’une parabole est la perpendiculaire à l’axe focal passant par le symétrique du foyer par rapport au sommet. Celle des coniques à centre est éloignée de ![]() du centre. Géométriquement, on obtient la directrice en construisant son pied sur l’axe focal qui est est le conjugué harmonique du foyer le plus proche par rapport aux deux sommets du diamètre.
du centre. Géométriquement, on obtient la directrice en construisant son pied sur l’axe focal qui est est le conjugué harmonique du foyer le plus proche par rapport aux deux sommets du diamètre.
Les lignes suivantes rassemblent des résultats d’un usage constant :
Les diamètres coupent les ordonnées en leur milieu (par définition).
Les ordonnées relatives à un même diamètre sont parallèles à la tangente au(x) sommet(s) de ce diamètre
Les diamètres conjugués ou, autrement dit, les côtés transverses conjugués ne sont définis que pour les coniques à centre. Ils sont parallèles aux ordonnées relatives au diamètre.
Les diamètres et les diamètres conjugués passent par le centre de la conique. Ils forment un repère par rapport auquel les équations de l’ellipse et de l’hyperbole sont réduites et respectivement ![]() et
et ![]() .
.
Les diamètres conjugués s’accompagnent d’un côté droit conjugué. Leurs longueurs respectives ![]() et
et ![]() sont déterminées par les égalités
sont déterminées par les égalités ![]() et
et ![]() . Ensemble, ils définissent une conique à centre dite conjuguée de la conique définie par le couple
. Ensemble, ils définissent une conique à centre dite conjuguée de la conique définie par le couple ![]() . Les égalités précédentes montrent que
. Les égalités précédentes montrent que ![]() et
et ![]() . L’ellipse et sa conjuguée forment une seule courbe car l’équation réduite est symétrique. En revanche, et bien qu’elles partagent les mêmes asymptotes, l’hyperbole se distingue de sa conjuguée.
. L’ellipse et sa conjuguée forment une seule courbe car l’équation réduite est symétrique. En revanche, et bien qu’elles partagent les mêmes asymptotes, l’hyperbole se distingue de sa conjuguée.
Les diamètres de la parabole sont parallèles entre eux.
Les asymptotes d’une hyperbole passent par le centre de la conique. Elles rencontrent les tangentes aux sommets du diamètre en des points éloignés d’une longueur ![]() du sommet, définie par l’égalité
du sommet, définie par l’égalité ![]() . Le nombre
. Le nombre ![]() est aussi celui de l’équation
est aussi celui de l’équation ![]() .
.
Les diamètres conjugués ont pour longueur le nombre ![]() des équations
des équations ![]() . C’est le second diamètre dans l’ellipse. Dans l’hyperbole, il a même longueur que le segment de tangente au sommet intercepté par les asymptotes.
. C’est le second diamètre dans l’ellipse. Dans l’hyperbole, il a même longueur que le segment de tangente au sommet intercepté par les asymptotes.
Le plan du Livre III et les outils utilisés
Le Livre III du Traité des Coniques présente une structure et une organisation logique assez simple.
En modernisant le propos, on peut résumer les six parties du Livre III de la manière suivante. Ce découpage ainsi que les sous-titres sont de notre fait et ne figurent pas dans le texte d’Apollonios.
La première partie rassemble les propositions 1 à 15 sous le titre « Les triangles ». Elle concerne des égalités d’aires de triangles et quadrilatères formés par les ordonnées d’un point d’une conique relativement à deux repères. On y utilise le groupe des propositions 42 à 45 du Livre I. Elles sont résumées plus loin lors de l’étude détaillée de cette partie.
La deuxième partie comporte les propositions 16 à 29 sous le titre « Les puissances ». Elle est consacrée aux propriétés des puissances que nous appellerons directionnelles d’un point par rapport à une conique. On y fait appel à la première partie « Les triangles » du Livre III. On trouve aussi des utilisations de I.21 (deuxième forme des relations caractéristiques de l’ellipse et de l’hyperbole), de I.60 (construction et définition des hyperboles conjuguées) et de II.11 (constance du produit des distances d’un point d’une hyperbole aux asymptotes dans la direction d’un diamètre).
La troisième partie rassemble les propositions 30 à 40 sous le titre « Le pôle et la polaire ». On y trouve la propriété générale de la division établie par une conique sur une sécante entre le pôle et sa polaire. On y utilise la première partie « Les triangles » du Livre III ainsi que des propriétés des livres précédents, principalement : I.20 et I.21 (deuxième forme des relations caractéristiques des coniques), I.37 et I.38 (propriété caractéristique du pied de la tangente en un point sur un diamètre ou sur le diamètre conjugué), II.8 (symétrie oblique des asymptotes) et II.12 (constance du produit des distances d’un point d’une hyperbole aux asymptotes dans des directions données).
La quatrième partie réunit les propositions 41 à 44 sous le titre « Les tangentes ». Elle traite de certaines propriétés des tangentes à une conique. On ne fait appel à aucune des propositions précédentes du Livre III, mais sont utilisées : I.35, I.37 et I.38 (propriété caractéristique du pied de la tangente en un point sur un diamètre ou sur le diamètre conjugué) et II.12 (constance du produit des distances d’un point d’une hyperbole aux asymptotes dans des directions données).
La cinquième partie comporte les propositions 45 à 52 sous le titre « Les foyers ». Elle concerne la définition et les principales propriétés des foyers, y compris la définition bifocale des ellipses et hyperboles. On y utilise principalement la proposition 42 de la partie précédente « Les tangentes » du Livre III.
Enfin la sixième partie réunit les propositions 53 à 56 sous le titre « La génération ». Elle est consacrée à la génération ponctuelle et/ou tangentielle des coniques, c’est-à-dire à la construction point par point d’une conique dont on connaît deux points avec leurs tangentes, et un autre point. Elle fait surtout appel aux propositions 16, 18, 20 de la deuxième partie « Les puissances » du Livre III.
Dans ce qui précède nous n’avons fait mention que des énoncés non triviaux, c’est-à-dire autres que les propositions supposées bien connues des Livres I et II (propriétés des diamètres et asymptotes, relations caractéristiques des coniques, etc…) dont on a pu trouver un résumé plus haut. Les références internes à chaque partie ne sont pas non plus indiquées.
Le contenu mathématique du livre III : les triangles (prop. 1 à 15)
Le Livre III s’ouvre sur une série de propositions destinés à évaluer les aires de triangles ou trapèzes délimités par des diamètres, des tangentes aux sommets et des ordonnées menées d’un ou de plusieurs points d’une conique. Ces polygones ont souvent comme sommet un point quelconque d’une conique et les deux côtés issus de ce point sont les ordonnées relativement à deux repères différents. Ces propositions permettent donc, entre autres, de faciliter les changements de repère. Le souci de généralité d’Apollonios le conduit à étudier pour chaque propriété les différents cas de figure obtenus suivant les positions de certains points, la nature de la conique considérée et l’utilisation de diamètres conjugués. D’autre part Apollonios transfère souvent ces propriétés à l’autre branche de l’hyperbole (qu’il considère – rappelons-le – comme une courbe différente) ainsi qu’à l’hyperbole conjuguée. Quand on considère que certains de ces cas manquent dans le texte apollonien et que, par ailleurs, certaines propositions ont été interpolées partiellement ou en entier, on aboutit à un groupe relativement touffu de propositions, dans lequel le lecteur moderne a quelque mal à se retrouver et où il a tendance à vouloir synthétiser les résultats obtenus. C’est cette synthèse que nous présentons ci-dessous avant de lire en détail les trois premières propositions.
Notations.
Pour effectuer cette synthèse et mieux observer l’aspect combinatoire et symétrique des résultats d’Apollonios nous avons introduit les notations suivantes. Un repère est défini le plus souvent par un diamètre noté (d1), passant par un sommet et la tangente notée (t1) en ce sommet qui donne la direction des ordonnées. De façon plus générale, le couple ((di),(ti)) représente le repère n°i. Cette situation se généralise au cas de l’hyperbole, où l’on a des repères dont le diamètre ne coupe pas la section. La direction des ordonnées est alors donnée par le diamètre conjugué.
Les points sont représentés par des lettres, mais les lettres indexées représentent des droites passant par ces points. Plus précisément, pour un point M quelconque, Mi désigne l’ordonnée passant par M relativement au repère ((di),(ti)).
tr(d1t1t2) désigne l’aire du triangle formé par les trois droites (d1), (t1) et (t2).
qu(t1M1M2d2) désigne l’aire du quadrilatère formé par les quatre droites (t1), (M1), (M2) et (d2).
Si ce quadrilatère est croisé, il s’agit de la différence des aires des triangles formés. En fait ce sont toujours des trapèzes, avec (t1)//(M1), et donc :
![]()
On trouvera sur les figures suivantes (fig. IVa1, IVa2, IVa3) des exemples de ces notations pour les 3 types de coniques.
L’ordre des propositions 1 à 15.
Les propositions 1 à 3 se rapportent à une situation sur une même conique quelconque.
Les propositions 4 à 12 concernent cette même situation sur des hyperboles opposées.
Les propositions 13 à 15 étudient enfin cette situation dans le cas des hyperboles conjuguées.
Les trois énoncés.
On peut regrouper les quinze propositions en trois types d’énoncés.
Le premier énonce la constance du triangle formé par deux tangentes et un diamètre :
![]()
Il est vrai sur une même section conique (prop. 1, fig. IVa 4, 5, 6) ou sur les hyperboles opposées (prop. 4, fig. IVa 7).
Dans la suite, sauf exception, on présentera dans les figures uniquement la situation de l’ellipse. Le lecteur pourra faire les figures correspondantes aux autres cas de figures.
Le deuxième énoncé concerne le «trapèze» obtenu à partir d’un point quelconque M de la conique. Ce trapèze est limité par, d’une part, les ordonnées issues de M correspondant à deux diamètres, et d’autre part, l’un des diamètres et la tangente au sommet de de l’autre diamètre. Ce trapèze est égal au triangle défini par cette tangente, le diamètre lui correspondant et l’ordonnée issue de M relative à l’autre repère.
![]()
Cette propriété est énoncée pour une même section (prop. 2, fig. IVa 8 pour un trapèze convexe, fig. IVa 9 pour un trapèze croisé), puis avec un second diamètre (prop.5 et 11), sur des branches d’hyperboles opposées (prop. 6) et enfin sur des hyperboles conjuguées (prop. 14 et 15).
On peut remarquer que si l’on place le point M au sommet de (d2) (intersection avec (t2)), l’énoncé (E2) revient à l’énoncé (E1), qui en est donc un cas particulier.
Enfin le dernier énoncé, le plus général, traite de l’égalité de trapèzes obtenus en deux points d’une conique, définis d’une part, par les deux ordonnées de ces points pour un repère et d’autre part, par l’ordonnée de l’un des points et le diamètre d’un autre repère.
![]()
Ce résultat est donné d’abord sur une même conique (prop. 3, fig. IVa 10), puis sur deux branches d’hyperboles opposées (prop. 7), dans certains cas particuliers (prop. 8, 9 et 10), avec un diamètre conjugué (prop. 12).



