Résumé du Livre II
Le Livre II ne considère plus les coniques dans l’espace mais comme des figures planes ayant des propriétés métriques caractéristiques. Il est consacré d’une part aux propriétés des asymptotes aux hyperboles, et d’autre part aux constructions des diamètres, axes, centres et tangentes à des coniques données. Le Livre II utilise essentiellement les relations entre ordonnées et abscisses, exposées aux propositions 11, 12, 13, 20 et 21 du Livre I. On a vu, dans notre commentaire du Livre I, que ces relations correspondent aux écritures suivantes, où $$$cd$$$ désigne le côté droit ou paramètre, et $$$ ct$$$ le côté transverse ou diamètre :
pour la parabole : $$$ y^2 = x \times cd$$$ ;
pour l’hyperbole : $$$ y^2 = x \times cd + (cd \times ct) \cdot \left ( \frac{x}{ct} \right )^2$$$ ou $$$ \frac {y^2}{x \times (x + ct)} = \frac{cd}{ct}$$$ ;
pour l’ellipse : $$$ y^2 = x \times cd - (cd \times ct) \cdot \left ( \frac{x}{ct} \right )^2$$$ ou $$$ \frac {y^2}{x \times (ct - x)} = \frac{cd}{ct}$$$.
La caractérisation du pied de la tangente comme conjugué harmonique du pied de l’ordonnée par rapport aux sommets est une autre propriété très usitée dans le Livre II. On la trouve dans les propositions 33, 34, 35, 36, 37 du Livre I et elle se traduit actuellement dans les écritures suivantes, où $$$a$$$ désigne l’abscisse du pied de la tangente sur le diamètre :
pour la parabole : $$$ a = -x$$$ ;
pour l’hyperbole, l’ellipse ou le cercle : $$$ \left \lvert x \pm \frac{ct}{2}\right \rvert \times \left \lvert a \pm \frac{ct}{2} \right \rvert = \left ( \frac{ct}{2} \right )^2$$$ ou $$$ \frac {y^2}{ \left (x \pm \frac{ct}{2} \right ) \times \left \lvert a \pm x \right \rvert}= \frac{cd}{ct}$$$.
Un grand nombre de propositions du Livre II utilise les propositions 46 à 51 du Livre I. Celles-ci permettent la découverte de nouveaux diamètres et ordonnées et la transformation correspondante des propriétés caractéristiques associées. Elles permettent de plus l’étude des hyperboles opposées (les deux branches de notre hyperbole) et des hyperboles conjuguées. Ces dernières ont été définies, à la soixantième et dernière proposition du Livre I : si on a une hyperbole de côté droit $$$cd$$$ et de côté transverse $$$ct$$$, alors l’hyperbole conjuguée a le même centre, échange ses abscisses et ordonnées avec l’hyperbole initiale, et possède un côté droit $$$ cd'$$$ et un côté transverse $$$ct'$$$ tels que : $$$ cd' \cdot ct' = (ct)^2$$$ et $$$ cd \cdot ct = (ct')^2$$$.
Le Livre II s’ouvre sur la définition d’une asymptote. Il s’agit d’une droite qui, conformément à l’étymologie, ne rencontre pas l’hyperbole. Elle passe par le centre et par un point situé sur la tangente au sommet d’un diamètre. Le carré de la distance de ce point au sommet est égal au quart de la "figure" (c’est-à-dire $$$ \frac{ct \times cd}{4}$$$). Les propositions suivantes démontrent que de telles droites ne rencontrent pas l’hyperbole, et que ce sont les meilleures possibles : au sens où toute droite issue du centre et comprise dans l’angle intérieur des asymptotes rencontre l’hyperbole. En outre les asymptotes sont les mêmes quel que soit le sommet choisi sur l’hyperbole. Apollonios décrit ensuite les propriétés des segments découpés sur une sécante par la courbe et les asymptotes : symétrie des asymptotes par rapport au diamètre, constance du produit des distances d’un point de la courbe aux asymptotes (c’est encore le quart de la figure). De même le produit des distances d’un point de l’hyperbole aux asymptotes sous deux directions données est constant.
La figure IIb1 et les égalités ci-dessous résument ces différentes propriétés.
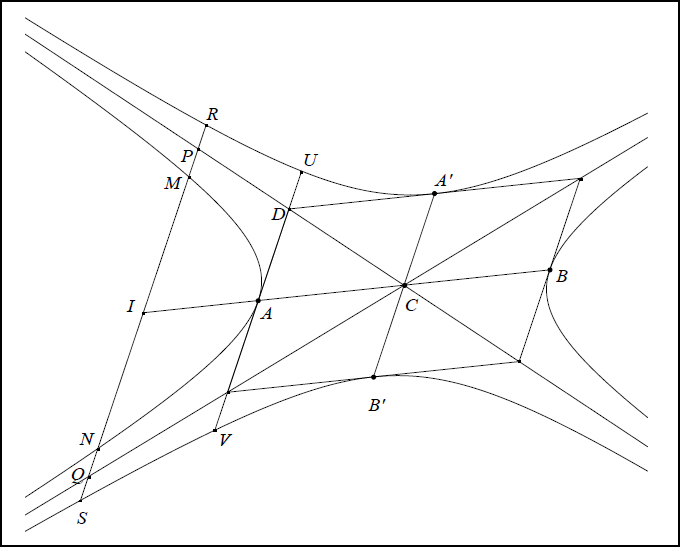
- Fig IIb 1
Livre I :
$$$ IM^2 = AI \cdot cd + (cd \cdot ct) \cdot \left ( \frac {AI}{ct} \right )^2$$$ (prop. 12) ;
$$$ \frac{IM^2}{IB \cdot IA} = \frac{cd}{ct}$$$ (prop. 21).
Livre II :
$$$ AD^2 = \frac{cd \times ct}{4}$$$ (prop. 1 et 22) ;
$$$ MP = NQ$$$ (prop. 8) ;
$$$ MP \cdot MQ = \frac{cd \times ct}{4}$$$ (prop. 10) ;
$$$ RP \cdot RQ = A'C^2$$$ (prop. 11) ;
$$$ RP = QS$$$ (prop. 16) ;
$$$ AU = AV$$$ (prop. 19) ;
$$$ MR \cdot MS = 2 \, CA'^2$$$ (prop. 23).
Avec ces propriétés, Apollonios démontre que la distance entre l’hyperbole et ses asymptotes peut être rendue plus petite que tout intervalle donné (proposition 14), ce que nous énoncerions : la distance entre l’hyperbole et ses asymptotes tend vers zéro. Cette proposition, l’une des rares de nature infinitésimale dans la géométrie grecque classique, n’est pas utilisée ailleurs dans le Livre II. Elle permet simplement de conclure que les asymptotes sont les droites les plus proches de l’hyperbole parmi celles qui ne la coupent pas.
Apollonios démontre ensuite (propositions 15 et 17) que ces asymptotes sont aussi celles de l’hyperbole opposée (l’autre branche de l’hyperbole) et celles des hyperboles conjuguées. La proposition 20 démontre que la définition (donnée plus haut) des hyperboles conjuguées ne dépend pas du diamètre choisi initialement.
Le groupe de propositions qui suit porte sur la situation des points d’intersection de deux tangentes ou de deux sécantes à diverses coniques. Les énoncés de ces propositions sont relativement simples mais les démonstrations, comme toutes celles de ce type dans la géométrie grecque, semblent liées à la considération de la figure. Apollonios démontre que dans la parabole, ou dans l’hyperbole, deux sécantes, dont les points de rencontre avec la conique ne s’entourent pas, se rencontrent à l’extérieur de la courbe (propositions 24 et 25). La figure IIb 2 illustre le cas de l’hyperbole quand les points ne s’entourent pas et la figure IIb 3 présente la situation où les points s’entourent.
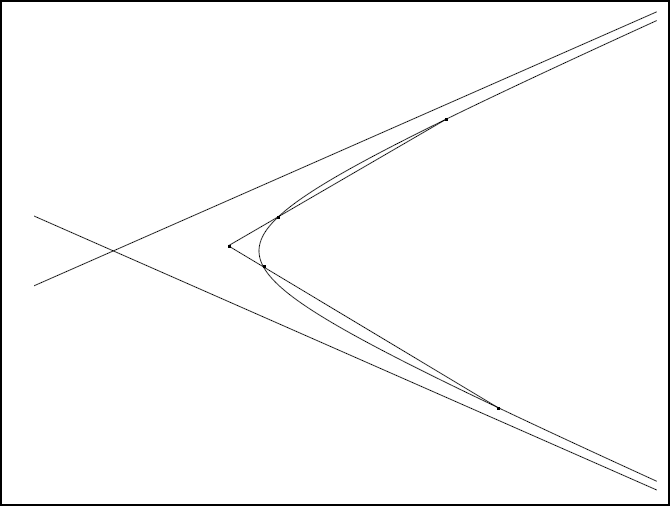
- Fig IIb 2
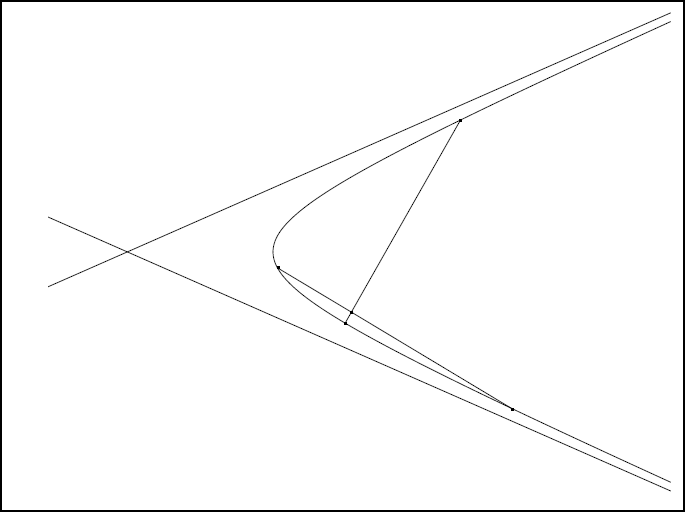
- Fig IIb 3
De même, deux tangentes à une ellipse sont soit parallèles soit sécantes du même côté que le centre par rapport à la droite joignant les points de contact (proposition 27). On a le même résultat pour l’hyperbole en considérant deux tangentes respectivement à chacune des branches opposées (proposition 31).
Enfin, on trouve dans ce Livre II un ensemble de résultats concernant les diamètres des coniques et leur construction à partir de sécantes ou de tangentes. Ainsi le parallélisme de la tangente au sommet avec la direction de la symétrie oblique par rapport au diamètre est plusieurs fois utilisé, ainsi que sa réciproque. Ceci permet de définir un diamètre comme l’ensemble des milieux de sécantes parallèles (propositions 28, 34, 36), et comme la droite joignant l’intersection de deux tangentes avec le milieu des points de contact (propositions 29, 30, 38, 39, 40). Ces propriétés sont démontrées pour toutes les coniques, et pour les deux branches d’une même hyperbole. Elles permettent aussi la construction des diamètres conjugués.
Le livre II s’achève sur d’autres problèmes de construction : trouver les diamètres, le centre, l’axe d’une conique donnée. Un diamètre est déterminé par les milieux de deux sécantes parallèles (proposition 44) ; le centre par l’intersection de deux diamètres déjà tracés (proposition 45) ; l’axe d’une parabole par un diamètre quelconque, une sécante perpendiculaire à ce diamètre : l’axe est parallèle au diamètre et passe par le milieu de la sécante perpendiculaire (proposition 46) ; l’axe d’une ellipse ou d’une hyperbole est déterminé par la médiatrice d’une corde joignant deux points à égale distance du centre (proposition 47).
Puis, la conique étant toujours donnée, il s’agit de tracer une tangente issue d’un point extérieur, et une tangente faisant un angle donné avec un diamètre. Cette dernière propriété revient à trouver dans une conique deux diamètres conjugués dont on donne l’angle. Apollonios donne les conditions, en particulier pour l’ellipse, que doit vérifier cet angle. La tangente issue d’un point extérieur est obtenue en faisant passer un diamètre par ce point et en en prenant le conjugué harmonique par rapport aux sommets. Cela donne le pied de l’ordonnée, dont la direction est la tangente au sommet (proposition 49).


