Interprétation moderne des relations d’Apollonios

L’étude des coniques se réduit maintenant à un savoir minimum. Les coniques à centre, en particulier, sont systématiquement étudiées dans le repère orthogonal défini sur l’axe focal avec le centre comme origine. Des calculs élémentaires établissent que les coordonnées $$$ (x , y)$$$ repérant un point d’une ellipse ou d’une hyperbole satisfont les équations $$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$$ ou $$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$$. On sait aussi interpréter les nombres figurant aux dénominateurs. Le « $$$a$$$ » mesure le demi-axe focal ; le « $$$b$$$ » mesure le petit axe de l’ellipse ou s’il s’agit d’une hyperbole, le segment de tangente allant du sommet de l’axe jusqu’au point de sa rencontre avec l’une des asymptotes. Tous ces éléments sont placés sur les figures (voir fig. IIc 1 pour l’ellipse et fig. IIc 2 pour l’hyperbole).

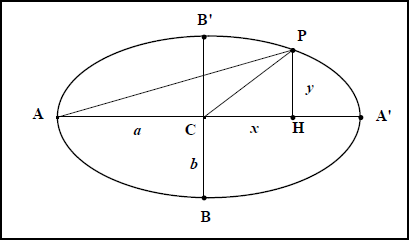
Fig IIc 1

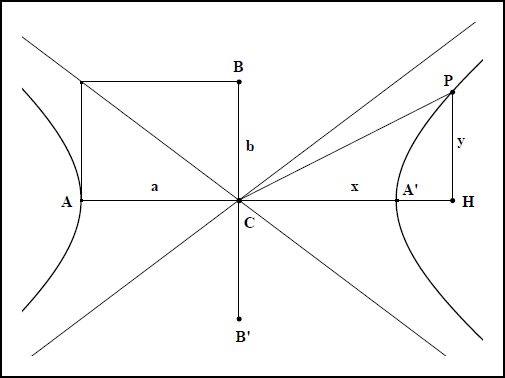
Fig IIc 2

Une expression des constantes $$$a$$$ et $$$b$$$ en fonction des constantes apolloniennes $$$cd$$$ et $$$ct$$$ est possible non seulement pour ce repère orthogonal, mais aussi pour tous les repères reposant sur les axes employés par Apollonios, c’est-à-dire, pour les repères dont les axes sont construits sur un diamètre et sur la tangente à l’un de ses sommets. Le qualificatif d’apollonien permet de distinguer ces repères et de simplifier le discours. Néanmoins, le lecteur gardera à l’esprit qu’il s’agit là d’un anachronisme commode, car le concept de repère n’appartient pas à l’époque d’Apollonios. Une translation d’un repère apollonien au centre de la conique, donne une repère formé sur les diamètres conjugués en raison du parallélisme de la tangente et du diamètre conjugué qui est aussi le second diamètre de l’ellipse. Le texte suivant se propose de montrer que la forme des équations réduites se maintient dans tout repère formé de deux diamètres conjugués. Auparavant, il se propose d’établir les relations entre les constantes « $$$a$$$ » et « $$$b$$$ », augmentées de quelques autres, et les constantes apolloniennes $$$ct$$$ et $$$cd$$$ et de montrer qu’elles sont indépendantes du repère formé sur deux axes conjugués.

Établir les relations entre les différentes constantes suppose que les équations réduites existent dans tout repère formé de deux diamètres conjugués. Sous cette hypothèse, l’entreprise n’est pas très difficile et se réduit à un simple jeu d’écriture. Elle repose sur la transformation de l’équation apollonienne lors d’une translation, au centre de la conique, du repère apollonien, construit sur le diamètre $$$AA'$$$ et sur la tangente au sommet $$$A$$$. Les éléments de la démonstration sont représentés sur les figures. Laissons de côté l’hyperbole qui nous mènerait à une répétition des arguments et considérons seulement l’ellipse. Les coordonnées d’un point courant P forment le couple $$$(x + a , y)$$$ dans le repère apollonien et le couple $$$(x , y)$$$ dans le repère utilisant le même jeu d’axes mais rapporté au centre, autrement dit dans le repère formé de deux diamètres conjugués.

Dans le premier repère, l’équation d’Apollonios s’écrit $$$ y^2 = cd \cdot (a + x) – \frac{cd}{ct} \cdot (a + x)^2$$$. D’où,

En utilisant, l’égalité $$$ ct = 2a$$$, il vient

Par identification avec $$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$$, on obtient

D’où, $$$ ct = 2a$$$ (on le savait déjà) et $$$ cd = \frac{2b^2}{a}$$$ .

En formant la proportion $$$ \frac{cd}{b} = \frac{2b}{a}$$$, la dernière égalité induit une construction simple de $$$ cd$$$.

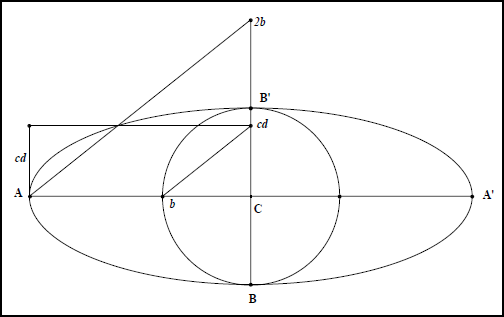
Fig IIc 3

Sur la figure IIc 3 le côté droit est reporté sur la tangente au sommet. Apollonios aurait choisi de le reporter sur une perpendiculaire au diamètre en l’un de ses sommets pour former un vrai rectangle de dimensions $$$x$$$ et $$$cd$$$, ou, en termes apolloniens, il forme le rectangle $$$AH \cdot HP$$$ en tant que surface qu’il compare à la surface carrée PH. La découverte de rapports irrationnels lui interdisait de passer d’une comparaison toujours licite entre des grandeurs géométriques à celle des nombres censés les mesurer, comme $$$x$$$ fois $$$cd$$$ et $$$ y^2$$$.

Par ailleurs, l’égalité $$$ \frac{cd}{ct} = \frac{b^2}{a^2}$$$ permet une expression de l’excentricité $$$e$$$ d’une conique à centre en fonction des nombres $$$cd$$$ et $$$ct$$$.

En effet, dans le cas de l’ellipse, $$$ \frac{cd}{ct} = \frac{b^2}{a^2} \Leftrightarrow \frac{ct - cd}{ct} = \frac{a^2 - b^2}{a^2} \Leftrightarrow \frac{ct - cd}{ct} = e^2$$$.

Dans le cas de l’hyperbole, $$$ \frac{cd}{ct} = \frac{b^2}{a^2} \Leftrightarrow \frac{ct + cd}{ct} = \frac{a^2 + b^2}{a^2} \Leftrightarrow \frac{ct + cd}{ct} = e^2$$$.

Le cas de la parabole est plus simple. Son équation réduite dans un repère orthonormé porté par l’axe et la tangente au sommet est de la forme $$$ y^2 = 2p \cdot x$$$. Donc, $$$ cd = 2p$$$. Comme $$$p$$$ est le double de la distance focale $$$f$$$ dans ce repère, nous avons aussi $$$ cd = 4 f$$$.

Dans un repère apollonien, seule l’égalité $$$ cd = 2p$$$ se conserve.

Constructions simples du côté droit

Le paragraphe précédent à montré comment passer des grandeurs apolloniennes $$$ct$$$ et $$$cd$$$ aux constantes apparaissant dans les équations modernes. Celui-ci se propose de représenter le côté droit à partir des grandeurs données dans le texte d’Apollonios, donc, indépendamment des équations réduites modernes. Le dessin du côté transverse ne posant pas de difficulté, la suite ne concerne que celui du côté droit. La construction proposée s’appuie sur celle de la moyenne géométrique. La figure II.c 4 illustre la construction de l’égalité $$$ h^2 = x \times y$$$. En fait, il faut y voir deux constructions, l’une ayant la moyenne géométrique $$$h$$$ pour inconnue, l’autre, l’un des facteurs $$$x$$$ ou $$$y$$$. Dans la situation où l’inconnue est $$$h$$$, le cercle de diamètre $$$AB = x + y$$$ intercepte la perpendiculaire $$$PH$$$ en $$$P$$$ et nous donne $$$h$$$. Dans celle où $$$y$$$ et $$$h$$$ sont connues, c’est la perpendiculaire $$$PA$$$ à l’hypoténuse qui nous donne $$$x$$$ et le cercle est inutile. La représentation du côté droit demande seulement de connaître la dernière construction.

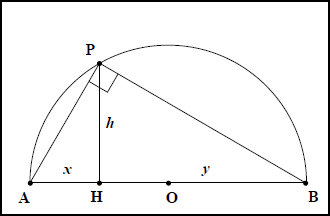
Fig IIc 4

Au préalable, rapportons les coordonnées d’un point du plan au repère construit sur un axe et sur la tangente à un sommet. Un point de la conique voit donc ses coordonnées satisfaire aux égalités apolloniennes $$$ y^2 = cd \cdot x - \frac{cd}{ct} \cdot x^2$$$ pour une l’ellipse et $$$ y^2 = cd \cdot x + \frac{cd}{ct} \cdot x^2$$$ pour une l’hyperbole. En particulier, les points de l’ellipse dont l’abscisse est $$$ \frac{ct}{2}$$$ , c’est-à-dire, les deux sommets du second diamètre, ont leurs coordonnées $$$ ( \frac{ct}{2} , y)$$$ qui vérifient l’égalité :

C’est une moyenne géométrique. De même, les points de l’hyperbole dont l’abscisse est $$$ct$$$ ont leurs coordonnées $$$ (ct , y)$$$ qui vérifient l’égalité $$$ y^2 = 2ct \times cd$$$. C’est une autre moyenne géométrique.

Dans l’ellipse, $$$ \frac{ct}{2}$$$ et $$$ y = OB^{\,*}$$$ sont connus. En reportant $$$OB^{\,*}$$$ sur la perpendiculaire, en $$$O$$$, au diamètre $$$AB$$$, la construction de la moyenne géométrique détermine le demi-côté droit sur $$$(AB)$$$. Un cercle de centre $$$O$$$ reporte le côté droit sur le diamètre conjugué et deux parallèles suffiraient à le reporter sur la tangente au sommet (voir figure IIc 5).

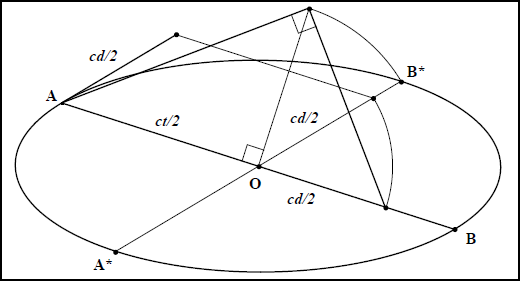
Fig IIc 5

Dans l’hyperbole, $$$ 2 \cdot ct$$$ et $$$y$$$ sont connus, l’un comme symétrique de $$$A$$$ par rapport à $$$B$$$, l’autre en traçant la parallèle à la tangente au sommet. En reportant $$$y$$$ sur la perpendiculaire, en $$$ x = ct$$$, au diamètre $$$AB$$$, la construction de la moyenne géométrique détermine le demi-côté droit sur $$$(AB)$$$ comme pour l’ellipse. Le côté droit se reporte ensuite sur l’ordonnée $$$y$$$, puis, à l’aide d’une parallèle au diamètre sur la tangente au sommet (voir fig. IIc 6).

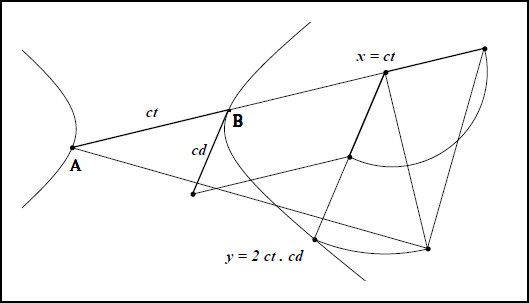
Fig IIc 6

La représentation du côté droit sur la figure d’une parabole procède d’une construction entièrement différente bien que le repère soit toujours formé d’un diamètre et de la tangente en son sommet. Les coordonnées d’un point courant sur la courbe satisfont donc à l’équation apollonienne $$$ y^2 = cd \cdot x$$$ et l’ordonnée du point d’abscisse $$$cd$$$ vérifie l’égalité $$$ y^2 = cd^2$$$. C’est toujours une moyenne géométrique mais sans grandeur connue à priori. Un changement de méthode s’impose et l’égalité $$$ x = y = cd$$$ suggère la construction d’un losange. Toute ordonnée étant parallèle à la tangente au sommet, une bissectrice de l’angle formé par la tangente au sommet et le diamètre rencontre la courbe en un point $$$P$$$ qui avec le sommet $$$A$$$ forme un losange dont les côtés ont même longueur que le côté droit (cf fig. IIc 7).

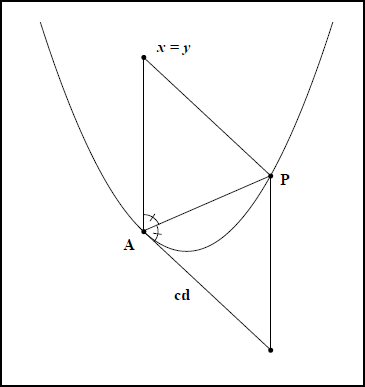
Fig IIc 7

Stabilité des équations réduites

La première partie de ce texte a montré les relations existant entre les constantes d’Apollonios $$$cd$$$ et $$$ct$$$ et les nôtres. L’argumentation reposait sur le fait que les égalités $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$ et $$$ \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$ reliant les coordonnées $$$(x , y)$$$ d’un point d’une conique à centre, ont la propriété d’exister dans tout repère formé par deux axes conjugués. Ce paragraphe propose une démonstration de cette propriété en s’appuyant sur la proposition 21 du livre I dont les résultats sont une généralisation aux cas de l’ellipse et de l’hyperbole de la propriété métrique fondamentale du cercle, à savoir, $$$ PH^2 = AH \cdot HB$$$. Les égalités numérotées (1) et (2) résument sous une forme moderne ceux qui concernent l’ellipse. Cette démonstration s’accompagne aussi d’un dessin définissant les différents éléments de l’argumentation (voir fig IIc 8).

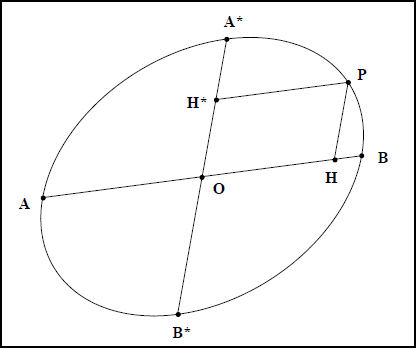
Fig IIc 8

$$$ \large \frac{{HP}^2}{\overline{AH} \cdot \overline{HB}} = \large \frac {{O{A}^*}^2}{{OA}^2} = \large \frac{cd}{ct} \qquad \normalsize{(1)}$$$

$$$ \large \frac{{{H}^*P}^2}{\overline{{A}^*{H}^*} \cdot \overline{{H}^*{B}^*}} = \large \frac {{OA}^2}{{O{A}^*}^2} = \large \frac{{cd}^*}{{ct}^*} \qquad \normalsize{(2)}$$$

Le point P formant le quatrième sommet d’un parallélogramme, nous obtenons les égalités suivantes :

$$$ {P{H}^*}^2 = HO^2 = (\overline{AO} - \overline{AH})(\overline{BO} - \overline{BH} )$$$

Soit : $$$ {P{H}^*}^2 = \overline{AO} \cdot \overline{OB} - \overline{AO} \cdot \overline{BH} - \overline{AH} \cdot \overline{BO} + \overline{AH} \cdot \overline{BH}$$$

Ou encore : $$$ {P{H}^*}^2 = \overline{AO} \cdot \overline{BO} - \overline{AO} \cdot (\overline{BH} + \overline{HA}) + \overline{AH} \cdot \overline{BH}$$$, car $$$ \overline{BO} = - \overline{AO}$$$.

C’est-à-dire : $$$ {P{H}^*}^2 = - AO^2 - 2\overline{AO} \cdot \overline{OA} + \overline{AH} \cdot \overline{BH}$$$, car $$$ \overline{BA} = 2\overline{OA}$$$.

Soit : $$$ {P{H}^*}^2 = AO^2 + \overline{AH} \cdot \overline{BH}$$$.

Ou : $$$ \large \frac{{P{H}^*}^2}{OA^2} = 1 + \large \frac{\overline{AH} \cdot \overline{BH}}{OA^2}$$$.

Soit : $$$ \large \frac{{P{H}^*}^2}{OA^2} = 1 - \large \frac{{HP}^2}{{O{A}^*}^2}$$$ , d’après l’égalité $$$ (1)$$$ car $$$ \overline{BH} = - \overline{HB}$$$.

Et finalement : $$$ \large \frac{{P{H}^*}^2}{{OA}^2} + \frac{{HP}^2}{{O{A}^*}^2} = \normalsize{1}$$$ c’est-à-dire, $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$.

Ce résultat est prouvé à partir de $$$ PH^{\,*}$$$ et en utilisant l’égalité $$$(1)$$$. Il pourrait se démontrer en partant de $$$PH$$$. Le raisonnement conserverait les mêmes articulations mais il considérerait les grandeurs de l’axe conjugué ($$$A^{\,*}B^{\,*}$$$) et l’égalité $$$(2)$$$ se substituerait à l’égalité $$$(1)$$$. Le lecteur pourra observer que la relation $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$ fait jouer un rôle parfaitement symétrique aux deux axes. Celui des abscisses est donc arbitraire et pourrait ne pas être le grand axe.

La stabilité des équations réduites liant les coordonnées d’un point d’une ellipse est maintenant démontrée dans tous les repères formés de deux diamètres conjugués. Le même résultat existe pour l’hyperbole et il se démontre de la même manière, mais en utilisant les relations de la proposition 21 qui, sous une forme moderne, se résument dans les égalités $$$(1')$$$ et $$$(2')$$$. Comme pour l’ellipse, le dessin annexe définit les autres éléments de la démonstration (cf. fig. IIc 9).

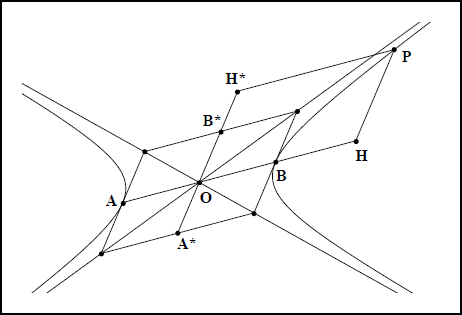
Fig IIc 9

$$$ \large \frac{{HP}^2}{\overline{AH} \cdot \overline{BH}} = \large \frac {{O{A}^*}^2}{{OA}^2} = \large \frac{cd}{ct} \qquad \normalsize{(1')}$$$

$$$ \large \frac{{{H}^*P}^2}{\overline{{A}^*{H}^*} \cdot \overline{{B}^*{H}^*}} = \large \frac {{OA}^2}{{O{A}^*}^2} = \large \frac{{cd}^*}{{ct}^*} \qquad \normalsize{(2')}$$$

Le raisonnement est en tout point identique au précédent, mais les propositions $$$(1')$$$ et $$$(2')$$$ entraînent que :

$$$ 1 + \large \frac{\overline{AH} \cdot \overline{BH}}{{OA}^2} = 1 + \large \frac{{HP}^2}{{O{A}^*}^2}$$$ et donc, que :

$$$ \large \frac{{P{H}^*}^2}{{OA}^2} - \frac{HP^2}{{O{A}^*}^2} = \normalsize{1} \Leftrightarrow \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$.

Le diamètre conjugué dans l’hyperbole

Le diamètre conjugué au côté transverse joue donc un rôle important dans l’étude des coniques. Nous avons choisi de le noter $$${ct}^*$$$ pour traduire l’expression côté transverse conjugué. Il est aussi, dans l’hyperbole comme dans l’ellipse, la longueur que, dans les équations réduites $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$ et $$$ \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$, nous notons $$$2b$$$. Toutefois, le diamètre conjugué $$${ct}^*$$$ n’a pas toujours sur la figure d’une hyperbole l’évidence qu’il a sur celle d’une ellipse. Il se voit bien quand les asymptotes sont données, car, en venant couper la tangente à l’un des sommets de l’axe, elles interceptent un segment de la longueur du diamètre conjugué. Sans les asymptotes, le diamètre conjugué n’est plus repérable. Il peut se construire à l’aide de la définition donnée par Apollonios, à savoir l’égalité $$$ cd \cdot ct = {ct^*}^2$$$ de laquelle, puisque $$$ {ct}^* = 2b$$$, on déduit l’égalité $$$ \large \frac{cd}{2} \cdot \frac{ct}{2} = \normalsize{b^2}$$$. Sa construction est donc à nouveau celle d’une moyenne géométrique.
Le texte suivant et la figure qui l’accompagne en proposent une construction sur la tangente au sommet B, quand les grandeurs connues sont le côté droit $$$cd$$$ et le côté transverse $$$ct$$$ (cf. fig IIc 10).

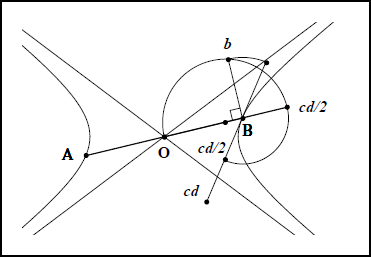
Fig IIc 10

À partir du sommet $$$B$$$, un arc de cercle reporte la longueur $$$ \large \frac{cd}{2}$$$ sur le grand axe, puis le cercle de diamètre $$$ \large \frac{cd}{2} + \frac{ct}{2}$$$ intercepte la perpendiculaire réalisant la moyenne géométrique de $$$ \frac{cd}{2}$$$ et de $$$ \large \frac{ct}{2}$$$, c’est-à-dire, en un point distant de $$$b$$$ du sommet $$$B$$$. Un arc de cercle reporte symétriquement la longueur $$$b$$$ sur la tangente au sommet. En plus de la longueur $$$2b$$$, ces deux points et le centre nous donnent les deux asymptotes.

Résumé

Pour la lecture et la compréhension du texte d’Apollonios, aucun des résultats précédents n’est vraiment nécessaire car l’étude faite par Apollonios se suffit à elle-même. Ils ne sont donnés que pour jeter un pont entre la manière moderne de voir les coniques et celle d’Apollonios, et afin de ne pas se sentir trop ignorant à la lecture d’énoncés formulant une mathématique d’un autre temps.

La suite propose un résumé des propriétés précédentes et de quelques autres. L’ensemble pouvant former un vade-mecum du lecteur d’Apollonios.

Les grandeurs $$$a$$$ et $$$b$$$, des équations $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$ et $$$ \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$, l’excentricité $$$e$$$ et la distance focale $$$f$$$ sont reliés au côté droit $$$cd$$$ et au côté transverse $$$ct$$$ par les égalités suivantes :

• $$$ ct = 2a$$$ ;
• $$$ cd = 2p$$$ pour la parabole. Lorsque le diamètre est l’axe focal, $$$cd = 4 \times f$$$ ;
• $$$ cd = \large \frac{2b^2}{a}$$$ pour les coniques à centre. Lorsque le diamètre est l’axe focal, la longueur $$$cd$$$ est aussi la distance entre les deux points de la courbe, symétriques par rapport au même foyer. Ainsi, la connaissance de l’une des grandeurs $$$cd$$$ ou $$$f$$$ permet la construction de l’autre ;
• $$$ \large \frac{cd}{ct} = \frac{b^2}{a^2}$$$.

La distance $$$c$$$ des foyers au centre d’une conique vérifie les égalités $$$ c^2 = a^2 + b^2$$$ pour l’hyperbole et $$$ c^2 = a^2 - b^2$$$ pour l’ellipse et pour ces deux coniques, les foyers sont les points dont l’ordonnée relative à l’axe focal mesure $$$ \large \frac{cd}{2}$$$.

Le quadruple de la distance focale d’une parabole est déterminée par l’abscisse d’un point commun à la courbe et à une bissectrice de l’angle que forment l’axe focal et la tangente au sommet. Cette abscisse valant $$$cd$$$, la distance focale vaut $$$ \large \frac{cd}{4}$$$.

• $$$ \large {\frac{ct - cd}{ct}} = \normalsize {e^2}$$$ pour l’ellipse, où $$$0$$$ < $$$e$$$ < $$$1$$$ ;
• $$$ \large {\frac{ct + cd}{ct}} = \normalsize {e^2}$$$ pour l’hyperbole où $$$1$$$ < $$$e$$$ ;
• pour la parabole, $$$ e = 1$$$.

La directrice d’une parabole est la perpendiculaire à l’axe focal passant par le symétrique du foyer par rapport au sommet. Celle des coniques à centre est éloignée de $$$ \large\frac{a^2}{c}$$$ du centre. Géométriquement, on obtient la directrice en construisant son pied sur l’axe focal qui est est le conjugué harmonique du foyer le plus proche par rapport aux deux sommets du diamètre.

Les lignes suivantes rassemblent des résultats d’un usage constant :

Les diamètres coupent les ordonnées en leur milieu (par définition).

Les ordonnées relatives à un même diamètre sont parallèles à la tangente au(x) sommet(s) de ce diamètre

Les diamètres conjugués ou, autrement dit, les côtés transverses conjugués ne sont définis que pour les coniques à centre. Ils sont parallèles aux ordonnées relatives au diamètre.

Les diamètres et les diamètres conjugués passent par le centre de la conique. Ils forment un repère par rapport auquel les équations de l’ellipse et de l’hyperbole sont réduites et respectivement $$$ \large \frac{x^2}{a^2} + \frac{y^2}{b^2} = \normalsize{1}$$$ et $$$ \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$.

Les diamètres conjugués s’accompagnent d’un côté droit conjugué. Leurs longueurs respectives $$${ct}^*$$$ et $$${cd}^*$$$ sont déterminées par les égalités $$${{ct}^*}^2 = cd \cdot ct$$$ et $$$ {ct}^2 = {cd}^* \cdot {ct}^*$$$. Ensemble, ils définissent une conique à centre dite conjuguée de la conique définie par le couple $$$(ct,cd)$$$. Les égalités précédentes montrent que $$$ {a}^* = b$$$ et $$$ {b}^* = a$$$. L’ellipse et sa conjuguée forment une seule courbe, car l’équation réduite est symétrique. En revanche, et bien qu’elles partagent les mêmes asymptotes, l’hyperbole se distingue de sa conjuguée.

Les diamètres de la parabole sont parallèles entre eux.

Les asymptotes d’une hyperbole passent par le centre de la conique. Elles rencontrent les tangentes aux sommets du diamètre en des points éloignés d’une longueur $$$b$$$ du sommet, définie par l’égalité $$$ {b}^2 = \large \frac{ct}{2} \times \frac{cd}{2}$$$. Le nombre $$$b$$$ est aussi celui de l’équation $$$ \large \frac{x^2}{a^2} - \frac{y^2}{b^2} = \normalsize{1}$$$.

Les diamètres conjugués ont pour longueur le nombre $$$2b$$$ des équations $$$ \large \frac{x^2}{a^2} \pm \frac{y^2}{b^2} = \normalsize{1}$$$. C’est le second diamètre dans l’ellipse. Dans l’hyperbole, il a même longueur que le segment de tangente au sommet intercepté par les asymptotes.