Le contenu mathématique du Livre III : les triangles (prop. 1 à 15)

lundi 26 décembre 2022
par  TrotouxD
popularité : 3%

Section précédente : Le plan du Livre III et les outils utilisés

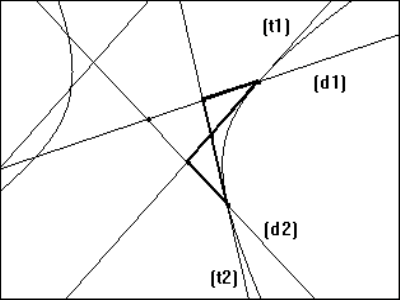
Les triangles

Le Livre III s’ouvre sur une série de propositions destinés à évaluer les aires de triangles ou trapèzes délimités par des diamètres, des tangentes aux sommets et des ordonnées menées d’un ou de plusieurs points d’une conique. Ces polygones ont souvent comme sommet un point quelconque d’une conique et les deux côtés issus de ce point sont les ordonnées relativement à deux repères différents. Ces propositions permettent donc, entre autres, de faciliter les changements de repère. Le souci de généralité d’Apollonios le conduit à étudier pour chaque propriété les différents cas de figure obtenus suivant les positions de certains points, la nature de la conique considérée et l’utilisation de diamètres conjugués. D’autre part Apollonios transfère souvent ces propriétés à l’autre branche de l’hyperbole (qu’il considère – rappelons-le – comme une courbe différente) ainsi qu’à l’hyperbole conjuguée. Quand on considère que certains de ces cas manquent dans le texte apollonien et que, par ailleurs, certaines propositions ont été interpolées partiellement ou en entier, on aboutit à un groupe relativement touffu de propositions, dans lequel le lecteur moderne a quelque mal à se retrouver et où il a tendance à vouloir synthétiser les résultats obtenus. C’est cette synthèse que nous présentons ci-dessous avant de lire en détail les trois premières propositions.

Notations

Pour effectuer cette synthèse et mieux observer l’aspect combinatoire et symétrique des résultats d’Apollonios nous avons introduit les notations suivantes. Un repère est défini le plus souvent par un diamètre (noté $$$(d_1)$$$), passant par un sommet et la tangente (notée $$$(t_1)$$$) en ce sommet qui donne la direction des ordonnées. De façon plus générale, le couple $$$(d_i,t_i)$$$ représente le repère n° $$$i$$$. Cette situation se généralise au cas de l’hyperbole, où l’on a des repères dont le diamètre ne coupe pas la section. La direction des ordonnées est alors donnée par le diamètre conjugué.

  • Les points sont représentés par des lettres, mais les lettres indexées représentent des droites passant par ces points.
  • Plus précisément, pour un point $$$M$$$ quelconque, $$$M_i$$$ désigne l’ordonnée passant par M relativement au repère $$$(d_i,t_i)$$$.
  • tr$$$(d_1t_1t_2)$$$ désigne l’aire du triangle formé par les trois droites $$$(d_1)$$$, $$$(t_1)$$$ et $$$(t_2)$$$.
  • qu$$$(t_1M_1M_2d_2)$$$ désigne l’aire du quadrilatère formé par les quatre droites $$$(t_1)$$$, $$$(M_1)$$$, $$$(M_2)$$$ et $$$(d_2)$$$. Si ce quadrilatère est croisé, il s’agit de la différence des aires des triangles formés. En fait ce sont toujours des trapèzes, avec $$$(t_1)$$$ // $$$(M_1)$$$, et donc :
qu$$$(t_1M_1M_2d_2)$$$ = $$$\lvert$$$tr$$$(t_1M_2d_2) -$$$tr$$$(M_1M_2d_2) \rvert$$$

$$$ \\ $$$

On trouvera sur les figures suivantes (fig. IVa 1, fig. IVa 2 et fig. IVa 3) des exemples de ces notations pour les trois types de coniques.

fig. IVa 1
fig. IVa 2
fig. IVa 3

L’ordre des propositions 1 à 15

Les propositions 1 à 3 se rapportent à une situation sur une même conique quelconque.
Les propositions 4 à 12 concernent cette même situation sur des hyperboles opposées.
Les propositions 13 à 15 étudient enfin cette situation dans le cas des hyperboles conjuguées.

Les trois énoncés

On peut regrouper les quinze propositions en trois types d’énoncés.

Le premier énonce la constance du triangle formé par deux tangentes et un diamètre :

$$$ \fbox {$ \large \textbf{(E}_{\textbf{1}}\textbf{)} \qquad \textbf{tr(d}_\textbf{1}\textbf{t}_{\textbf{1}}\textbf{t}_\textbf{2}\textbf{)=}\textbf{tr(d}_\textbf{2}\textbf{t}_{\textbf{2}}\textbf{t}_\textbf{1}\textbf{)} $}$$$

$$$ \\ $$$

Il est vrai sur une même section conique (prop. 1, fig. IVa 4, fig. IVa 5 et fig. IVa 6) ou sur les hyperboles opposées (prop. 4, fig. IVa 7).

fig. IVa 4
fig. IVa 5
fig. IVa 6
fig. IVa 7

Dans la suite, sauf exception, on présentera dans les figures uniquement la situation de l’ellipse. Le lecteur pourra faire les figures correspondant aux autres coniques.

Le deuxième énoncé concerne le « trapèze » obtenu à partir d’un point quelconque $$$M$$$ de la conique. Ce trapèze est limité par, d’une part, les ordonnées issues de $$$M$$$ correspondant à deux diamètres, d’autre part, l’un des diamètres et la tangente au sommet de l’autre diamètre. Ce trapèze est égal au triangle défini par cette tangente, le diamètre qui lui correspond et l’ordonnée issue de $$$M$$$ relative à l’autre repère.

$$$ \fbox {$ \large \textbf{(E}_{\textbf{2}}\textbf{)} \qquad \textbf{qu(t}_\textbf{1}\textbf{M}_{\textbf{1}}\textbf{M}_\textbf{2}\textbf{d}_{\textbf{2}}\textbf{)=}\textbf{tr(t}_\textbf{1}\textbf{M}_{\textbf{2}}\textbf{d}_\textbf{1}\textbf{)} $}$$$

$$$ \\ $$$

Cette propriété est énoncée pour une même section (prop. 2, fig. IVa 8 pour un trapèze convexe, fig. IVa 9 pour un trapèze croisé), puis avec un second diamètre (prop. 5 et prop. 11), sur des branches d’hyperboles opposées (prop. 6) et enfin sur des hyperboles conjuguées (prop. 14 et prop. 15).

On peut remarquer que si l’on place le point $$$M$$$ au sommet de $$$(d_2)$$$ (intersection avec $$$(t_2)$$$), l’énoncé $$$(\textrm{E}_2)$$$ revient à l’énoncé $$$(\textrm{E}_1)$$$, qui en est donc un cas particulier.

fig. IVa 8
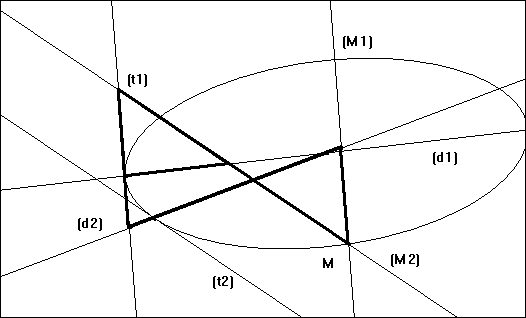
fig. IVa 9

Enfin le dernier énoncé, le plus général, traite de l’égalité de trapèzes obtenus en deux points d’une conique, définis d’une part, par les deux ordonnées de ces points et d’autre part, par l’ordonée de l’un des points et le diamètre d’un autre repère.

$$$ \fbox {$ \large \textbf{(E}_{\textbf{3}}\textbf{)} \qquad \textbf{qu(M}_\textbf{1}\textbf{N}_{\textbf{1}}\textbf{N}_\textbf{2}\textbf{d}_{\textbf{2}}\textbf{)=}\textbf{qu(N}_\textbf{2}\textbf{M}_{\textbf{2}}\textbf{M}_\textbf{1}\textbf{d}_{\textbf{1}}\textbf{)} $}$$$

$$$ \\ $$$

Ce résultat est donné d’abord sur une même conique (prop. 3, fig. IVa 10), puis sur deux branches d’hyperboles opposées (prop. 7), dans certains cas particuliers (prop. 8, prop. 9. et prop. 10), avec un diamètre conjugué (prop. 12).

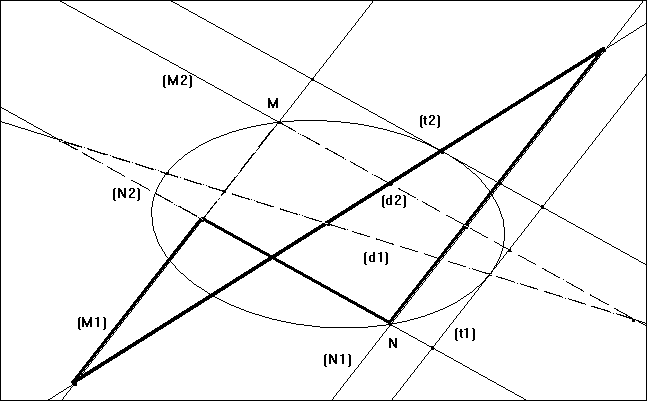
fig. IVa 10

On peut remarquer que si l’on place le point $$$M$$$ au sommet de $$$(d_1)$$$, alors l’énoncé $$$(\textrm{E}_3)$$$ devient l’énoncé $$$(\textrm{E}_2)$$$, qui en est donc un cas particulier.

Ces 15 propositions expriment donc diverses formes d’une propriété générale des coniques. Nous n’avons pas voulu considérer les cas particuliers (dont certains ne sont pas plus évoqués par Apollonios que par nous) du genre : que se passe-t-il si $$$(d_1)$$$ et $$$(d_2)$$$ sont perpendiculaires ?

Lecture des trois premières propositions.

Avant de commencer notre lecture, il convient de donner brièvement le contenu des propositions 42 à 45 du Livre I. Ces propositions démontrent dans différents cas (proposition 42 pour la parabole, proposition 43 pour les coniques à centre, proposition 44 pour les deux branches de l’hyperbole, proposition 45 pour un diamètre conjugué) le même résultat : le triangle formé à partir d’un point quelconque d’une conique entre les ordonnées issues de ce point et le diamètre du premier repère est égal au quadrilatère (trapèze ou différence de triangles homothétiques pour une conique à centre, parallélogramme pour une parabole) formé par les deux diamètres, la tangente au sommet du premier repère et l’ordonnée du premier repère issue du point. Avec les notations introduites ci-dessus, on obtient l’énoncé :

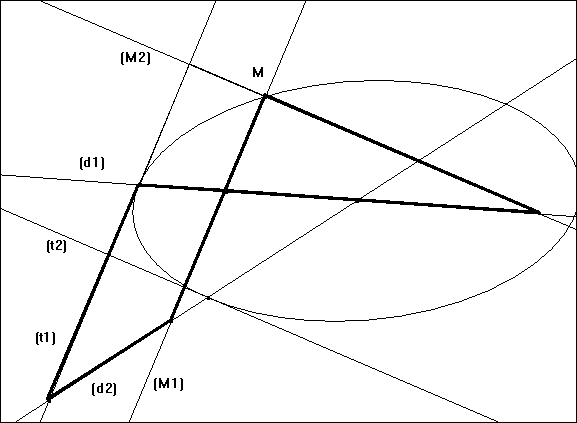
$$$ \fbox {$ \large \textbf{(E}_{\textbf{0}}\textbf{)} \qquad \textbf{tr(M}_\textbf{1}\textbf{M}_{\textbf{2}}\textbf{d}_{\textbf{1}}\textbf{)=}\textbf{qu(t}_{\textbf{1}}\textbf{M}_{\textbf{1}}\textbf{d}_{\textbf{1}}\textbf{d}_{\textbf{2}}\textbf{)} $}$$$

$$$ \\ $$$

fig. IVa 11

Les démonstrations utilisent principalement les propriétés issues de la division harmonique définie sur un diamètre par une tangente (Livre I, propositions 35 et 39).

Micheline Decorps-Foulquier a montré dans sa thèse (XXX, pp. 154-162), à partir des commentaires d’Eutocius et d’un lemme de Pappus que ces démonstrations avaient été sans doute écrites initialement par Apollonios de façon progressive : un premier énoncé, qui pouvait faire l’objet d’une proposition intermédiaire entre I.42 et I.43 démontrait que pour une conique à centre :

$$$ \large \textbf{(E}_{\textbf{0,1}}\textbf{)} \qquad \textbf{tr(d}_\textbf{1}\textbf{d}_{\textbf{2}}\textbf{t}_{\textbf{1}}\textbf{)=}\textbf{tr(d}_{\textbf{2}}\textbf{d}_{\textbf{1}}\textbf{t}_{\textbf{2}}\textbf{),}$$$

$$$ \\ $$$

résultat qui apparaît dans la variante d’Eutocius de la démonstration de I.43, et que des commentateurs ont interpolé ensuite dans la proposition III.1 (cf. fig. IVa 12). On peut noter qu’Apollonios donne cet énoncé pour des hyperboles conjuguées (prop. 13, fig. IVa 13).

fig. IVa 12

fig. IVa 13

Le deuxième énoncé démontre un résultat équivalent au précédent :

$$$ \large \textbf{(E}_{\textbf{0,2}}\textbf{)} \qquad \textbf{tr(d}_\textbf{1}\textbf{t}_{\textbf{2}}\textbf{B}_{\textbf{1}}\textbf{)=}\textbf{qu(t}_{\textbf{1}}\textbf{B}_{\textbf{1}}\textbf{d}_{\textbf{1}}\textbf{d}_{\textbf{2}}\textbf{)}$$$

$$$ \\ $$$
en notant $$$B$$$ le sommet de ($$$d_2$$$) (cf. fig. IVa 14).

fig. IVa 14

Ce résultat est d’ailleurs un cas particulier de l’énoncé ($$$E_0$$$) ci-dessus, si l’on place le point $$$M$$$ au sommet du deuxième repère.

D’un point de vue plus moderne, on peut dire que l’énoncé ($$$E_0$$$) exprime la constance de l’aire d’un certain quadrilatère quelle que soit la position du point $$$M$$$ sur la conique. Mais il faut noter que ce quadrilatère n’est plus un trapèze et il faut entendre la valeur absolue de la somme ou de la différence des aires des triangles tr$$$(M_1M_2d_1)$$$ et tr$$$(d_1d_2M_1)$$$, la somme étant faite dans le cas de l’ellipse, la différence dans le cas de l’hyperbole (cf. fig IVa 15).

$$$ \fbox {$ \large \textbf{(E'}_{\textbf{0}}\textbf{)} \qquad \left \lvert \textbf{tr(}\textbf{M}_\textbf{1}\textbf{M}_\textbf{2}\textbf{d}_\textbf{1}\textbf{)} \pm \textbf{tr(}\textbf{d}_\textbf{1}\textbf{d}_\textbf{2}\textbf{M}_\textbf{1}\textbf{)} \right \rvert \textbf{=} \, \textbf{tr(}\textbf{d}_\textbf{1}\textbf{d}_\textbf{2}\textbf{t}_\textbf{1}\textbf{)}$}$$$

$$$ \\ $$$
Figure IVa 15

Nous pouvons maintenant commencer la lecture des trois premières propositions.

À suivre...