À partir de l’étude d’un cahier de navigation écrit par un pilote du Havre pendant sa détention lors de la Guerre de Sept ans, D. Trotoux a exposé comment les logarithmes découverts au début du XVIIe siècle ont été très vite utilisés et appliqués dans un domaine pratique, celui de la navigation, pour inventer un instrument graphique appelé échelle anglaise ou règle de Gunter, que l’on peut considérer comme un ancêtre de la règle à calcul. La règle de Gunter appelée plus simplement Gunter a été utilisée pour la navigation jusqu’au milieu du XIXe siècle dans les pays anglo-saxons.
On trouvera à la fin de cet article le diaporama présenté lors de l’exposé.
Le Cahier de navigation de Jean-Baptiste Le Grip (1762)
En juin 2019, un cahier de navigation manuscrit écrit par un pilote du Havre, Jean-Baptiste Le Grip, a été acquis par la bibliothèque de la ville du Havre puis numérisé au cours du dernier trimestre de l’année 2019, ce qui a rendu son accès facile et permis son étude.
On peut consulter le manuscrit sur le site web de l’Association Science en Seine et Patrimoine (ASSP) . Le Cayez de Navigation est constitué de plus de 350 pages, il comporte 140 illustrations et diagrammes et 6 volvelles, disques mobiles en papier pivotant les uns sur les autres destinés à simplifier les calculs d’événements cycliques, notamment pour la navigation. Il a été écrit par Jean-Baptiste Le Grip pendant sa captivité (1761-1763) au château de Sissinghurst (Kent) durant la Guerre de Sept ans (1756-1763).
Pour en savoir plus sur la vie de Jean-Baptiste Le Grip :
La navigation par l’Échelle Anglaise
La partie du manuscrit étudiée concerne "l’Échelle Anglaise" :
- Navigation par la grande Échelle Anglaise et démonstrations par la petite ;
- Questions astronomiques par l’Échelle Anglaise.
Ces deux parties occupent environ 70 pages soit environ un cinquième de l’ouvrage.
La première partie traite de problèmes de trigonométrie plane utiles pour la navigation : réductions de lieues mineures en lieues majeures [1], calcul de la moyenne parallèle entre deux latitudes données et problèmes généraux de navigation (calculs de l’air de vent [2], du chemin parcouru, des coordonnées du point d’arrivée d’une route donnée, etc.).
La deuxième partie, quant à elle, traite des problèmes de trigonométrie sphérique : détermination de la déclinaison et de l’ascension droite du Soleil [3], de ses heures de lever et coucher et de l’azimut et l’heure d’observation connaissant la déclinaison et la hauteur du Soleil au-dessus de l’horizon.
Cette Échelle Anglaise n’est décrite par Le Grip que dans la première proposition sans être illustrée par un schéma. Voici ce que l’on peut lire :
En premier lieu il faut savoir et connaître les cordes de l’échelle qui est composée de cinq cordes dont la première à la main droite est la corde des huit rumbs de vent où est marqué SR qui veut dire sinus des rumbs de vent. La deuxième corde est la corde des nombres marquée NUM ou la corde des lieues. La troisième corde est la corde de sinus ou de 90° marquée SIN. La quatrième corde de la tangente où est marqué 45°, marquée TAN ou la prendre aussi pour 90°. La cinquième corde est la corde des méridiennaux qui sert à trouver la moyenne parallèle marquée MER.
La consultation du Nouveau traité de navigation de Pierre Bouguer (1753) a permis de comprendre que les cordes en question étaient des échelles ou graduations logarithmiques et qu’elles étaient d’une grande utilité pour le calcul du quatrième terme d’une proportion dont on connaît les trois premiers termes et que l’Échelle Anglaise était une règle sur laquelle on trouvait ces différentes graduations.
Pourquoi cette dénomination d’Échelle Anglaise ?
Trois mathématiciens anglais ont joué un rôle majeur dans l’histoire de cette Échelle Anglaise :
- John Napier (1550-1617), inventeur du concept de logarithmes et auteur des premières tables dans sa Mirifici logarithmorum canonis descriptio en 1614.
- Henry Briggs (1556-1630), calculateur et auteur de la première table logarithmique à base décimale Logarithmorum chilias prima en 1617 reprise et complétée dans son Arithmetica Logarithmica en 1624.
- Edmund Gunter (1581-1626), auteur en 1620 du Canon triangulorum… table contenant ses propres logarithmes décimaux des sinus et des tangentes nouvellement calculés et les logarithmes des nombres de Briggs et inventeur de la méthode des échelles logarithmiques dans Description and use of the sector en 1624.
C’est le nom de Gunter qui est passé à la postérité grâce à sa nouvelle table d’échelles logarithmiques puis son ingéniosité d’en faire des graduations sur des règles dites de Gunter ou tout simplement, Gunters.
L’apport d’Edmund Gunter
Gunter fut nommé professeur d’astronomie au collège de Gresham en 1619. C’était un savant actif dans de nombreux domaines en particulier l’astronomie et la navigation. Il s’intéressait aux applications des mathématiques et était, de plus, un fervent partisan du système décimal.
La loi des sinus : $$$\frac{x}{sin(X)} =\frac{y}{sin(Y)}$$$, qui était l’une des opérations les plus utiles en navigation pour déterminer les côtés et les angles d’un triangle ne pouvait pas être utilisée directement avec les tables de Napier, ni avec les tables de Briggs. En 1620, Gunter publia la première table combinée, le Canon Triangulorum… et désormais, la règle des sinus pouvait enfin être appliquée en utilisant les logarithmes des tables d’un seul livre.
Gunter a poursuivi ensuite ses recherches estimant que certains problèmes de navigation nécessitaient une solution plus simple et plus rapide que ne le permettait le calcul par tables. Cela l’a conduit à concevoir un nouveau type d’échelle où les nombres étaient représentés par des distances d’échelle logarithmique et où un compas à pointes sèches était utilisé pour ajouter et soustraire ces distances dans le domaine logarithmique.
Dans son ouvrage Use of the Sector...(1624), Gunter a proposé trois échelles logarithmiques pour faciliter les calculs de proportions. D’abord l’échelle logarithmique des nombres notée N, mais aussi l’échelle logarithmique des sinus, notée S et celle des tangentes, notée T, afin que la règle des sinus puisse être appliquée. Il a également proposé l’ajout d’une quatrième échelle logarithmique des sinus verses pour faciliter certains calculs de trigonométrie sphérique.
Description and use of the sector, the cross-staff and other instruments, London, 1624
La règle de Gunter
La règle de Gunter standard est le plus souvent en bois, mais parfois en laiton et des exemplaires d’un pied de long en ivoire ont été recensés. La majorité des règles de Gunter connues ne portent ni nom de fabricant ni date de fabrication. Bien sûr, on rencontre des variations, comme les échelles avec des abréviations de noms différentes, des échelles étendues mais aussi des tailles différentes. La plupart des règles de Gunter mesurent deux pieds de long sur 2 pouces ou 1 pouce et demi de large (soit environ 610 x 50 mm). Il existe des modèles d’un pied, avec les mêmes échelles que la règle de Gunter standard réduites dans cette plus petite taille.
Description de la règle de Gunter de 2 pieds
La règle de Gunter est graduée sur ses deux faces. Nous décrirons successivement la face recto, puis la face verso.
- Face recto de la règle de Gunter
Le bord supérieur de la face recto de la règle comporte une échelle de mesure graduée de la droite vers la gauche de 0 à 24 pouces.
Sur la partie gauche figure une échelle diagonale qui sert à prendre les longueurs précises avec le compas en centièmes de pouces et de demi-pouces pour construire les différentes graduations de la règle.
Sur la partie droite, on trouve un certain nombre de graduations (principalement trigonométriques) dont aucune n’est logarithmique.
Le tableau suivant donne un résumé du nom et de la signification des principales graduations (la colonne « Formule » donne la longueur proportionnelle sur une graduation pour un nombre X sur cette échelle).
| Nom abrégé de la graduation | Nom complet | Signification | Formule |
|---|---|---|---|
| LEA | Lieues | Graduation linéaire des tracés de distances nautiques | |
| RUM | Cordes [4] des rumbs | La corde vaut 2 fois le sinus du demi-angle pour les points cardinaux de la boussole (32 en 360°) | $$$2sin(5,625X)$$$ |
| CHO | Cordes [4] des degrés | La corde vaut 2 fois le sinus du demi-angle pour les degrés | $$$2sin(\frac{X}{2})$$$ |
| SIN | Sinus des degrés | Sinus de l’angle | $$$sin(X)$$$ |
| SEC | Sécantes des degrés | Sécante de l’angle | $$$sec(X)$$$ |
| TAN | Tangentes des degrés | Tangente de l’angle | $$$tan(X)$$$ |
| S*T | Semi-tangente des degrés | Tangente du demi-angle | $$$tan(\frac{X}{2})$$$ |
| LON ou M*L | Milles de longitudes | Longueur d’un degré à la latitude X° | $$$60cos(X)$$$ à combiner avec la graduation CHO située dessous |
- Face verso de la règle de Gunter
Sur la face verso de la règle de Gunter figurent des graduations logarithmiques (sauf les deux dernières) dont on donne un résumé du nom et de la signification ci-dessous.
| Nom abrégé de la graduation | Nom complet | Signification | Formule |
|---|---|---|---|
| S*R | Sinus artificiels [5] des rumbs | log sinus des 8 premiers points cardinaux de la boussole | $$$log(sin(11,25X))$$$ |
| T*R | Tangentes artificielles [5] des rumbs | log tangente des 4 premiers points cardinaux de la boussole | $$$log(tan(11,25X))$$$ |
| NUM | Ligne des nombres artificiels [5] | Graduation logarithmique à 2 cycles (comme les échelles A et B de nos règles à calcul "modernes" | $$$log(X)$$$ |
| SIN | Sinus artificiels [5] des degrés | log sinus des degrés (360°) | $$$log(sin(X))$$$ |
| V*S | Sinus Verses artificiels [5] des degrés | log sinus verse des degrés (360°) | $$$log(1-sin^2(\frac{X}{2}))$$$ |
| TAN | Tangentes artificielles [5] des degrés | log tangente des degrés (360°) | $$$log(tan(X))$$$ |
| MER | Ligne Méridionale | « Accroissement du degré de latitude » sur un méridien de la carte de Mercator | $$$\int {sec(X)dX}$$$ à combiner avec E*P |
| E*P | Parties égales | Graduation linéaire | $$$X$$$ |
Utilisation de la règle de Gunter
Soit la proportion $$$A:B::C:D$$$ (qui se lit $$$A$$$ est à $$$B$$$ comme $$$C$$$ est à $$$D$$$) où $$$A$$$, $$$B$$$ et $$$C$$$ sont donnés. Comment obtenir $$$D$$$ ?
Écrivons cette proportion sous la forme $$$\frac{A}{B}=\frac{C}{D}$$$ ou en utilisant les logarithmes :
$$$log(A)-log(B)=log(C)-log(D)$$$.
On peut alors interpréter la proportion comme l’égalité de la distance entre $$$log(A)$$$ et $$$log(B)$$$ et de celle entre $$$log(C)$$$ et $$$log(D)$$$.
Avec un compas à pointes sèches, la distance entre $$$log(A)$$$ et $$$log(B)$$$ s’obtient en écartant les pointes du compas entrer les valeurs $$$A$$$ et $$$B$$$ de l’échelle logarithmique. Il suffit alors, en gardant cet écart, de déplacer le compas de sorte qu’un de ses pieds soit placé en $$$log(C)$$$, c’est-à dire sur la valeur $$$C$$$ de l’échelle logarithmique. L’autre pied du compas tombera alors en $$$log(D)$$$. On peut alors lire directement la valeur $$$D$$$ en ce point sans avoir à utiliser le logarithme inverse.
On peut imaginer le temps gagné par rapport à l’ancienne méthode où il fallait lire dans la table $$$log(A)$$$, $$$log(B)$$$ et $$$log(C)$$$, puis effectuer le calcul $$$log(C)-(log(A)-log(B))$$$ pour obtenir $$$log(D)$$$ et enfin $$$D$$$ par lecture inverse de la table.
Pour illustrer cette pratique, prenons deux exemples dans l’ouvrage d’Edmund Stone, The construction and principal uses of mathematical instruments publié à Londres en 1723. Cet ouvrage est une traduction de l’ouvrage Traité de la construction et des principaux usages des instruments de mathématiques de Nicolas Bion (1709), complété par la construction et l’utilisation des instruments que celui-ci n’avait pas recensés, principalement ceux inventés et perfectionnés par les Anglais, en particulier la règle de Gunter.
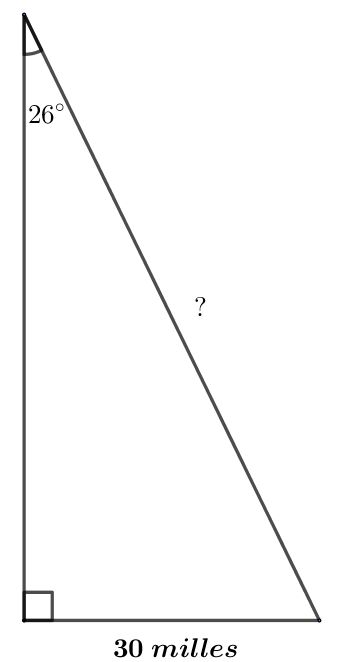
Exemple 1 : Étant donnés la base d’un triangle rectangle de 30 milles et l’angle opposé à celle-ci de 26 degrés, trouver la longueur de l’hypoténuse.
Comme le sinus de l’angle, 26 degrés, est à la base, 30 milles, ainsi le rayon est à la longueur de l’hypoténuse. Placez un pied de votre compas sur le 26e degré de la ligne des Sinus, et étendez l’autre à 30 sur la ligne des Nombres ; le compas restant ainsi ouvert, placez un pied sur 90 degrés, ou sur la fin de la ligne des Sinus et faites-en sorte que l’autre tombe sur la ligne des Nombres, ce qui donnera 68 milles et demi environ, pour la longueur de l’hypoténuse cherchée.
Explication : On a $$$\frac{sin \,26°}{30} =\frac{sin \, 90°}{x}$$$ soit $$$log(sin \,26°)-log(30) = log(sin \, 90°)-log(x)$$$.Le premier membre de l’égalité correspond à la première ouverture du compas et le second membre à l’ouverture reportée. Sur l’échelle des nombres, on peut lire environ 70 milles sous la pointe gauche du compas (celui représenté en rouge).
On peut remarquer que l’égalité précédente peut aussi s’écrire : $$$log(sin \, 90°)-log(sin \,26°) =log(x)-log(30)$$$, ce qui permet de prendre la première ouverture sur l’échelle SIN et de la reporter sur l’échelle NUM. On voit ici l’intérêt d’avoir placé ces deux échelles l’une au-dessus de l’autre de manière adjacente ce qui permet, dans ce cas, de n’avoir à déplacer le compas qu’horizontalement le long de la ligne commune de ces deux échelles.
Exemple 2 : Étant donnés la base d’un triangle rectangle de 25 milles et la perpendiculaire de 15 milles, trouver l’angle opposé à cette perpendiculaire.
Comme la base 25 milles est à la perpendiculaire 15 milles, ainsi le rayon est à la tangente de l’angle cherché ; car si la base est faite rayon, la perpendiculaire serait la Tangente de l’angle opposé à la perpendiculaire. Ouvrez votre compas sur la ligne des Nombres, de 15, la perpendiculaire donnée, à 25, la base donnée, et la même ouverture sera obtenue en sens inverse, sur la ligne des Tangentes, de 45 degrés à 31 degrés, l’angle recherché.
Explication : On a $$$\frac{25}{15} =\frac{1}{tan \,\theta} = \frac{tan \,45°}{tan \, \theta}$$$ soit $$$log(25)-log(15) = log(tan \,45°)-log(tan \, \theta)$$$. Le premier membre de l’égalité correspond à la première ouverture du compas et le second membre à l’ouverture reportée. Sur l’échelle des tangentes, on peut lire environ 31° sous la pointe gauche du compas (celui représenté en rouge).
Cas de la trigonométrie sphérique
La loi des sinus de la trigonométrie sphérique (qui s’applique aussi bien au triangles rectangles qu’aux triangles obliques) s’écrit : $$$\frac{sin\,A}{sin\,a}=\frac{sin\,B}{sin\,b}$$$ où $$$A$$$ et $$$B$$$ sont les angles aux sommets du triangle et $$$a$$$ et $$$b$$$, les segments des grands cercles qui leur sont opposés (c’est-à-dire les côtés du triangle). Les angles et les côtés sont mesurés en degrés.
En utilisant les logarithmes, cette égalité peut être vue au choix comme : $$$log(sin \, A) - log(sin \, a) = log( sin \, B ) - log(sin \, b)$$$ ou $$$log(sin \, A) - log(sin \, B) = log(sin \, a) - log(sin \, b)$$$.
Les règles utilisées pour la résolution des triangles sphériques possédant un ou plusieurs angles droits, expriment des proportions qui relient le rapport des sinus à l’un ou l’autre des autres rapports de sinus ou des proportions qui relient les rapports des sinus aux rapports des tangentes.
Ainsi, les mêmes procédures fonctionneront, en utilisant une paire de distances sur la ligne des sinus et une autre sur la ligne des tangentes.
Pour les triangles sphériques obliques où un CAC, CCC ou AAA [6] est impliqué, la situation est plus compliquée et l’utilisation de la ligne des sinus verses peut être envisagée.
Exemple 3 : Étant donnés l’hypoténuse d’un triangle sphérique rectangle de 60 degrés, par exemple, et un des côtés de 20 degrés, trouver l’angle opposé à ce côté.
Comme le sinus de l’hypoténuse 60 degrés est au rayon, ainsi le sinus du côté donné 20 degrés est au sinus de l’angle recherché. Ouvrez votre compas, sur la ligne des Sinus, de 60 degrés au rayon ou 90 degrés, et la même ouverture sera obtenue sur la ligne des Sinus dans le même sens, de 20 degrés, le côté donné, à 23 degrés 10 minutes, la quantité de l’angle recherché.
Explication : Par la formule $$$sin\,c=sin \,a \times sin \, C$$$, on a $$$\frac{sin \, 60°}{1} =\frac{sin \, 20°}{sin \,C} = \frac{sin \, 60°}{sin \, 90°}$$$, ce qui peut aussi être écrit sous la forme $$$log(sin \, 90°)-log(sin \, 60°) = log(sin \,C)-log(sin \, 20°)$$$. Le premier membre de l’égalité correspond à la première ouverture du compas et le second membre à l’ouverture reportée. Sur l’échelle des sinus, on peut lire environ 24° sous la pointe droite du compas (celui représenté en rouge).
Fabrication d’une réplique de la règle de Gunter
Ayant compris la fabrication et l’utilisation de cette règle, il était tentant de la mettre à l’épreuve des problèmes de navigation proposés à titre démonstratif par Le Grip dans son manuscrit, pour en déterminer la précision. Une première réplique de la règle a été réalisée à l’aide d’une règle en carton de 40 cm sur laquelle avaient été collées des photocopies des faces recto et verso de la règle. Il s’est avéré à l’usage que la précision obtenue avec cette réplique, à savoir un degré, était très loin de celle indiquée par Le Grip, la minute. Il a alors été décidé de fabriquer une réplique en bois à l’échelle 1/1 de la règle de Gunter.
-
Dans un premier temps, des plans des graduations de chaque face ont été réalisés à l’aide du logiciel $$$Geogebra^{®}$$$ et enregistrés au format vectoriel .svg.
-
Ensuite ces fichiers ont été importés dans le logiciel de dessin vectoriel $$$Inkscape^{®}$$$ pour y insérer les noms des différentes graduations et indiquer les valeurs numériques.
-
La dernière étape s’est déroulée au FabLab Le Dôme de Caen où il a été possible d’utiliser une découpeuse laser. Le matériau utilisé est du contreplaqué de peuplier d’épaisseur 5 mm. Le fichier .svg est chargé dans le logiciel $$$Inkscape^{®}$$$ et on choisit comme pilote d’impression celui de la découpeuse laser et, une fois les réglages effectués, on utilise le logiciel qui pilote la découpeuse laser. C’est la couleur de tracé des traits qui détermine le travail effectué par la découpeuse laser (dans notre cas, Rouge = découpe, Bleu = gravure fine pour les graduations et Noir = surface gravée pour les noms des échelles et les valeurs numériques).
Avec cette nouvelle réplique de la règle, la précision obtenue est nettement améliorée (environ 15 minutes) sans atteindre toutefois la précision affichée dans le texte de Legrip. On ne peut qu’être admiratif devant le savoir-faire et la précision du travail des facteurs d’instruments des XVIIe et XVIIIe siècles et on peut émettre l’hypothèse que certaines valeurs indiquées par Le Grip avaient été calculées à l’aide d’autres méthodes que l’utilisation de la règle de Gunter puisqu’un même problème pouvait être repris pour illustrer différentes méthodes de calcul (par le quartier de réduction, par le quartier sphérique, par les sinus logarithmes...), ce qui expliquerait cette différence de précision.
Documents annexes
Bibliographie
- Pierre Bouguer, Nouveau traité de navigation contenant la théorie et la pratique du pilotage, Paris, 1753.
- Joel Silverberg, The Plain and Gunter’s Scales – Seventeenth Century Additions to the Toolbox of Students and Practitioners of the Mathematicks, MAA/AMS Joint Mathematical Meetings, Baltimore, 01/2014.
- Edmund Stone, The construction and principal uses of mathematical instruments translated from the French of M. Bion, chief instrument-maker to the French king, to which are added, the constructions and uses of such instruments as are omitted by M. Bion ; particularly of those invented or improved by the English, London, 1723 (traduction des pages consacrées à l’échelle de Gunter).
- Otto Van Poelje, Gunter Rules in Navigation, Journal of the Oughtred Society, Vol. 13, N° 1, Spring 2004, p. 11-22, (traduction).
- Évelyne Barbin et al., Histoires de logarithmes, Ellipses, Paris, 2006.
- Le dossier Naviguer par l’échelle anglaise sur le site de l’ASSP : http://assprouen.fr/.
- La documentation du projet sur le site du Fab Lab Le Dôme de Caen